1. Визначаються кінцева мета моделювання, сукупність чинників|факторів| і показників, їх ролі: які з|із| них можна вважати|лічити| вхідними (тими, що пояснюють), а які вихідними (тими, що можна пояснити), збору|збирання| статистичної інформації.
2. Постулювання, математична формалізація, перевірка початкових|вихідних| припущень.
3. Власне моделюючий. Виведення загального|спільного| виду модельних співвідношень, зв'язаних між собою вхідними і вихідними показниками.
4. Статистичний аналіз моделі. Рішення задач якнайкращого|щонайкращого,найкращого| підбору, тобто статистичне оцінювання невідомих параметрів, що входять до аналітичного запису моделі, і дослідження властивостей одержаних|отриманих| оцінок, їх точності.
5. Верифікація моделі. Зіставлення висновків|укладень,ув'язнень|, оцінок, наслідків і висновків|виведень| з|із| реально спостережуваною дійсністю.
6. Дослідження спрямовані на уточнення моделі (залежить від результатів моделювання).
2. Нормальний розподіл. Цей вид розподілу має більшість ознак сільськогосподарських і біологічних об'єктів із|із| безперервним характером|вдачею| варіювання. Він не залежить від розмірності ознаки. Характерна|вдача| особливість нормального розподілу полягає в тому, що чим більше відхиляється значення окремої варіанти від середньої арифметичної, тим рідше вона зустрічається, тим менше її вірогідність|ймовірність| появи в генеральній сукупності. Навпаки, чим ближче варіанти до середнього значення ряду|лави,низки|, тим частіше вони зустрічаються, тим більша вірогідність|ймовірність| їх появи. Інакше кажучи, частота відхилень (від середнього значення) є|з'являється,являється| функцією їх величини. Ця закономірність у розподілі варіант характеризується плавною кривою, яка називається «кривою нормального розподілу ».
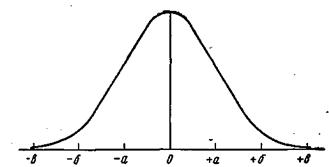
Рис. 5 – Крива нормального розподілу
При аналізі цього графіка (рис. 5) звертає на себе увагу симетричність кривої: це свідчить про те, що в нормальному розподілі великі і малі значення ознаки зустрічаються однаково часто. Оскільки|тому що| крива не перетинає осі абсцис, то можуть бути вельми|дуже| значні відхилення від середнього значення, проте|однак| вірогідність|ймовірність| їх появи дуже мала. Місцеположення точок перегину кривої, що визначають її форму, залежить від ступеня|міри| варіювання значень ознаки. Криву нормального розподілу можна побудувати|спорудити|, користуючись формулою (19):
 (19)
(19)
де Y – ордината кривої; N – об'єм|обсяг| сукупності; σ|β,α³λ| – середнє квадратичне відхилення; х – відхилення від середньої арифметичної; е – основа натурального логарифма (е=2,71).
3. Обчислення|підрахунок| теоретично очікуваних|сподіваних| частот нормального розподілу. Про форму розподілу будь-якого емпіричного ряду|лави,низки| можна мати певне уявлення|виставу,подання,представлення|, побудувавши|спорудивши| графік розподілу фактичних (тих, що отримані внаслідок експерименту); при цьому на осі ординат відкладають у відомому масштабі чисельності, а на осі абсцис – градації ознаки, що варіюють. Наведена на рис. 6 суцільна лінія (фактичні частоти) в основних рисах|межах| нагадує криву нормального розподілу. Тому з|із| відомою підставою|основою,заснуванням| можна вважати|лічити|, що ця ознака – число колосків у колосі – має нормальний розподіл.
Проте|однак| в деяких дослідженнях представляє|уявляє| інтерес визначення теоретично очікуваних|сподіваних| частот нормального розподілу. При цьому буде одержана|отримана| відповідь на питання: яку частоту мала б кожна градація ознаки за умов, що|при умові, що,при условии | їх розподіл нормальний.
| Частоти | 
|
| Число колосків у колосі |
Рис. 6 – Криві розподілу: а – емпірична; б – теоретична
Порівняння емпіричних і теоретичних частот дозволить зробити обґрунтований висновок|виведення| про форму розподілу сукупності, що вивчається. Крім того, теоретичний розподіл, може мати самостійне значення як математичне очікування|чекання| частот у генеральній сукупності.
Таблиця 17 – Розрахунок теоретичних частот за рівнянням нормального розподілу
| Число колосків в колосі (х) | Частота фактична f | а | fa | fa2 | τ | Ордината (за положен-ням І) | Частота теоретично розрахована, Yo |
| –5 | –10 | 2,74 | 0,0093 | ||||
| –4 | –68 | 2,20 | 0,0355 | ||||
| –3 | –75 | 1,65 | 0,1023 | ||||
| –2 | –116 | 1,12 | 0,2131 | ||||
| –1 | –76 | 0,58 | 0,3372 | ||||
| 0,04 | 0,3986 | ||||||
| 0,49 | 0,3538 | ||||||
| 1,03 | 0,2347 | ||||||
| 1,56 | 0,1192 | ||||||
| 2,11 | 0,0431 | ||||||
| 2,64 | 0,0122 | ||||||
| X | - | - |
Для обчислення|підрахунку| теоретично очікуваних|сподіваних| частот користуються рівнянням (20), яке можна перетворити таким чином:
 (20)
(20)  (21)
(21)
де Y0 – очікувана|сподівана| частота; τ – нормоване відхилення.
Для полегшення розрахунків необхідно користуватися спеціальними таблицями|, в яких розраховані значення другого співмножника рівняння для τ від 0 до 4,00. Теоретична частота визначається шляхом перемноження відношення 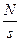 на коефіцієнт, відповідний кожному значенню τ (додаток 1).
на коефіцієнт, відповідний кожному значенню τ (додаток 1).
4. Обчислення|підрахунок| критерію А.Н. Колмогорова. Критерій А.Н. Колмогорова заснований на оцінці найбільшої різниці між накопиченими частотами емпіричного і теоретичного розподілів. Для розподілу 500 колосів озимої пшениці Білоцерківська 198 за кількістю плодовитих|плодючих,плідних| колосків обчислені|обчисляти,вичислені| «теоретичні» частоти, які вписані в графу 3 табл. 17. Відповідні розрахунки наведені в 4, 5 і 6-й графах табл. 18.
Таблиця 18 – Емпіричний і теоретичний розподіли колосів озимої пшениці за числом колосків у колосі
| Число колосків у колосі | Частоти | Накопичені частоти | |D| | ||
| емпіричні | теоретичні | емпіричні | теоретичні | ||
| Сума | - | - |
Критерій А.Н. Колмогорова (λ), обчислюється за формулою:
 (22)
(22)
де |D| – максимальна абсолютна різниця між накопиченими (так званими «інтегральними») частотами емпіричного і теоретичного розподілу для однієї і тієї ж групи; N – загальна|спільна| чисельність сукупності.
 .
.
Емпіричний розподіл неістотно|несуттєво| відхиляється від нормального в тих випадках коли λ<1,36, а при суворому підході, коли λ<1,63. Граничне значення критерію  , де ln – натуральний логарифм числа
, де ln – натуральний логарифм числа  ; β – рівень значущості. Так, якщо прийняти β =0,05, то
; β – рівень значущості. Так, якщо прийняти β =0,05, то  . У даному випадку величина критерію вказує|вказує| на те, що не буде погрішністю вважати|лічити| нормальним розподіл колосів за числом колосків у даному досліді|досліді|. На рис. 2 наведені криві обох розподілів табл. 18.
. У даному випадку величина критерію вказує|вказує| на те, що не буде погрішністю вважати|лічити| нормальним розподіл колосів за числом колосків у даному досліді|досліді|. На рис. 2 наведені криві обох розподілів табл. 18.
5. Закономірності нормального розподілу. Крива нормального розподілу (рис. 1) є графічним відображенням вірогідності|ймовірності| для будь-якого значення з|із| нескінченно великої сукупності й знаходиться|перебуває| в певних межах. Крива має найбільшу ординату в точці|точці|, яка відповідає місцеположенню на осі абсцис середньої арифметичної ( ). Отже, в нормально розподіленій сукупності найчастіше зустрічаються її представники із|із| значенням ознаки, що дорівнює
). Отже, в нормально розподіленій сукупності найчастіше зустрічаються її представники із|із| значенням ознаки, що дорівнює  , тобто вона має найбільшу вірогідність|ймовірність| знаходитися|перебувати| в сукупності. Крива нормального розподілу симетрична щодо|відносно| ординати
, тобто вона має найбільшу вірогідність|ймовірність| знаходитися|перебувати| в сукупності. Крива нормального розподілу симетрична щодо|відносно| ординати  , тому вірогідність|ймовірність| знаходження в сукупності величин, що однаково відхиляються від
, тому вірогідність|ймовірність| знаходження в сукупності величин, що однаково відхиляються від  в ту або іншу сторону, рівна. З іншого боку, в міру збільшення відхилень від середньої (у більший або менший бік) вірогідність|ймовірність| їх появи поступово зменшується. Оскільки|тому що| крива ніде не перетинається з|із| віссю абсцис, то, взагалі кажучи, можливо наявність відхилень, що як завгодно|бажано| відрізняються від
в ту або іншу сторону, рівна. З іншого боку, в міру збільшення відхилень від середньої (у більший або менший бік) вірогідність|ймовірність| їх появи поступово зменшується. Оскільки|тому що| крива ніде не перетинається з|із| віссю абсцис, то, взагалі кажучи, можливо наявність відхилень, що як завгодно|бажано| відрізняються від  ; проте|однак| вірогідність|ймовірність| появи як дуже малих, так і дуже великих відхилень незначна.
; проте|однак| вірогідність|ймовірність| появи як дуже малих, так і дуже великих відхилень незначна.
Якщо уважно розглянути|розгледіти| рис. 5, то не важко|скрутно| відмітити|помітити|, що симетрична крива має по два перегини з кожного боку від осі симетрії. Цим крапкам|точки| характерна чудова властивість: ординати їх визначають вірогідності|ймовірності| знаходження в сукупності значень ознаки, що відхиляються від  на величини, кратні середньому квадратичному відхиленню. Так, точка –а визначає вірогідність|ймовірність| відхилень від
на величини, кратні середньому квадратичному відхиленню. Так, точка –а визначає вірогідність|ймовірність| відхилень від  величину, меншу за σ, точка +а – на величину, більшу за σ. Відповідно точки –б і +б – на –2σ і +2σ, точки –в і +в – на –3σ і +3σ. У теоретичній статистиці доводиться, що:
величину, меншу за σ, точка +а – на величину, більшу за σ. Відповідно точки –б і +б – на –2σ і +2σ, точки –в і +в – на –3σ і +3σ. У теоретичній статистиці доводиться, що:
1) площа|майдан|, обмежена знизу відрізком осі абсцис від –σ до +σ, а зверху – відповідною частиною|часткою| кривої, дорівнює приблизно 2/3 всієї площі|майдану| розподілу, а отже, включає таку ж кількість варіант. Точні обчислення|підрахунки| показують, що в межах від – σ до +σ знаходиться|перебуває| 68,26 %, за цими межами – 31,74 % всіх варіант;
2) у межах від –2σ до +2σ знаходиться|перебуває| 95,46 %, поза|зовні| цією межею тільки|лише| 4,54 % всієї кількості варіант;
3) у межах від –3σ до +3σ знаходиться|перебуває| 99,74 %, тобто|цебто| практично всі варіанти.
На основі цієї закономірності можна обчислити|обчисляти,вичислити| вірогідність|ймовірність| відхилення будь-якої варіанти від середньої арифметичної. Наприклад, вірогідність|ймовірність| того, що випадково взята з|із| сукупності варіанта відрізняється від середньої не більше, ніж на величину середнього квадратичного відхилення, буде (з|із| розрахунку від 1000 випадків) 683:1000, тобто|цебто| Р = 0,683, а вірогідність|ймовірність| того, що воно відрізнятиметься на величину більшу за σ, дорівнює 0,317. Щоб визначити вірогідність|ймовірність| знаходження варіант у відомих межах, які визначаються величиною σ|β,α³λ|, користуються спеціальними таблицями, обчисленими за рівнянням нормального розподілу (табл. 19). Табл. 19 є|з'являється,являється| двосторонньою|двобічною|, оскільки|тому що| за нею визначається вірогідність|ймовірність| появи варіант по обидва боки від середньої арифметичної. У ній величини х позначають|значать| відхилення від  в одиницях σ|β,α³λ|.
в одиницях σ|β,α³λ|.
Таблиця 19 – Вірогідність|ймовірність| знаходження варіант в межах ±хσ(А) і поза|зовні| межами ±хσ(А) з|із| розрахунку на 1000 випадків
| х | Р(х) | х | Р(х) | х | Р(х) | х | Р(х) | ||||
| А | В | А | В | А | В | А | В | ||||
| 0,10 | 1,10 | 2,10 | 3,10 | ||||||||
| 0,20 | 1,20 | 2,20 | 3,20 | ||||||||
| 0,30 | 1,30 | 2,30 | 3,30 | ||||||||
| 0,40 | 1,40 | 2,40 | 3,40 | ||||||||
| 0,50 | 1,50 | 2,50 | 3,50 | ||||||||
| 0,60 | 1,60 | 2,58 | |||||||||
| 0,67 | 1,64 | 2,60 | |||||||||
| 0,70 | 1,80 | 2,70 | |||||||||
| 0,80 | 1,90 | 2,80 | |||||||||
| 0,90 | 1,96 | 2,90 | |||||||||
| 1,00 | 2,00 | 3,00 |
Примітка|тлумачення|. У графах А і В нуль цілих, для скорочення об'єму|обсягу| таблиці, опущений. Наприклад 451 слід читати як 0,451.
При оцінці істотності результатів дослідів найчастіше користуються рівнем достовірності|ймовірністю| 0,95 або рівнем значущості 0,05. Звертаючись|обертаючись| до табл. 19, не важко|скрутно| відмітити|помітити|, що Р(х)=0,95 відповідає х=1,96. Отже, вірогідність|ймовірність| того, що в нормальному розподілі відхилення від середньої  не перевищить величину 1,96, рівна 0,95, а вірогідність|ймовірність| того, що воно буде більше 1,96σ, дорівнює 0,05. Наведемо декілька прикладів|зразки| використання поняття про статистичну вірогідність|ймовірність| для вирішення практичних завдань|задач|.
не перевищить величину 1,96, рівна 0,95, а вірогідність|ймовірність| того, що воно буде більше 1,96σ, дорівнює 0,05. Наведемо декілька прикладів|зразки| використання поняття про статистичну вірогідність|ймовірність| для вирішення практичних завдань|задач|.
Приклад|зразок| 1. При дослідженні варіювання врожаю зерна (на одну рослину) у|в,біля| сорту|гатунку| ярової пшениці Харківської 46 одержані|отримані| такі характеристики:  =2,36 г і s=l,331 г. Серед рослин цього сорту|гатунку| було одне вагою зерна 6,64 г, що відхиляється від
=2,36 г і s=l,331 г. Серед рослин цього сорту|гатунку| було одне вагою зерна 6,64 г, що відхиляється від  на 6,64–2,36=4,28 г. Таке значне відхилення викликає|спричиняє| деякий сумнів у приналежності цієї рослини до даної сукупності. Для перевірки обчислюємо|обчисляємо,вичисляємо| х=4,28:1,331=3,22 і, звертаючись|обертаючись| до таблиці 3, знаходимо|находимо|, що варіанту з|із| врожаєм 6,64 г можна віднести до цього ряду|лави,низки| з|із| вірогідністю|ймовірністю| P(х)=0,999. Інакше кажучи, у вибірці з|із| 1000 рослин може зустрітися тільки|лише| одне з|із| врожаєм 6,64 г.
на 6,64–2,36=4,28 г. Таке значне відхилення викликає|спричиняє| деякий сумнів у приналежності цієї рослини до даної сукупності. Для перевірки обчислюємо|обчисляємо,вичисляємо| х=4,28:1,331=3,22 і, звертаючись|обертаючись| до таблиці 3, знаходимо|находимо|, що варіанту з|із| врожаєм 6,64 г можна віднести до цього ряду|лави,низки| з|із| вірогідністю|ймовірністю| P(х)=0,999. Інакше кажучи, у вибірці з|із| 1000 рослин може зустрітися тільки|лише| одне з|із| врожаєм 6,64 г.
Приклад|зразок| 2. Місце розташування нижнього бобу гороху пов'язане з довжиною вегетаційного періоду. У|в,біля| ранніх сортів|гатунків| він розташовується на 9–11-му, у|в,біля| середньостиглих – на 12–13-му і у|в,біля| пізньостиглих – на 19–24-му вузлі|лічивши| знизу. Цю сортову особливість використовують для виділення домішок|нечистот|.
Оскільки|тому що| вказані вище цифри є середніми величинами і у кожному окремому випадку під впливом умов зростання можуть дещо змінюватися, то проводять спеціальний математичний аналіз, що дозволяє виділити «помилкові» варіанти.
Так були одержані|отримані| дані про варіювання числа вузлів до першого бобу у|в,біля| сорту|гатунку| гороху Вікторія Мандорфська (табл. 20).
Таблиця 20 – Розподіл рослин гороху за місцеположенням першого бобу
| Число вузлів до першого бобу | |||||||||||
| Число рослин |
Обчисливши|обчисляючи,вичисливши|  =13,0 вузлів і s=l,19 вузла, і рівні значущості 0,01 (якому за таблицею 3 відповідає х=2,58), знаходимо|находимо| межі випадкових коливань місцеположення нижніх бобів:
=13,0 вузлів і s=l,19 вузла, і рівні значущості 0,01 (якому за таблицею 3 відповідає х=2,58), знаходимо|находимо| межі випадкових коливань місцеположення нижніх бобів:  ±2,58s, тобто|цебто| від 10 до 16 міжвузлів|. Отже, рослини, у|в,біля| яких нижній біб|біб| розташований|схильний| на 8, 9, 17 і 18-му міжвузлі|, можна вважати|лічити| домішками|нечистотами|, що належать до інших сортів|гатунків|.
±2,58s, тобто|цебто| від 10 до 16 міжвузлів|. Отже, рослини, у|в,біля| яких нижній біб|біб| розташований|схильний| на 8, 9, 17 і 18-му міжвузлі|, можна вважати|лічити| домішками|нечистотами|, що належать до інших сортів|гатунків|.
Якщо використовувати інший рівень істотності (це вирішує|рішає| сам дослідник), наприклад 0,05, то слід віднести до даного ряду|лави,низки| варіанти, що знаходяться|перебувають| в межах х±1,965 s, тобто|цебто| від 10,6 до 15,3 вузла. За цими межами буде 19 рослин, близько 4 % загальної|спільної| чисельності.
Таблиці для знаходження вірогідності|ймовірності|, відповідної різним значенням τ, є|з'являються,являються| односторонніми|однобічними|, оскільки|тому що| вони розраховані тільки|лише| для однієї половини кривої нормального розподілу. Визвлікання з|із| більш обширноїтаблиці одностороннього|однобічного| критерію наведене в табл. 5. На відміну від таблиці 3 її числа представляють|уявляють| накопичені частоти нормального розподілу від 0 до τ. Так, τ=2,0 відповідає число 4772; це означає|значить|, що 47,72 % варіант знаходиться|перебуває| між ординатами τ=0 і τ=2,0. Якщо помножити числа таблиці на 2, то одержимо|отримаємо| вірогідність|ймовірність| знаходження варіанти в межах ±2τ, тобто|цебто| ті ж величини, що і в табл. 21. Все вищесказане про розрахунок вірогідності|ймовірності| відноситься до достатньо|досить| великих вибірок із|із| сукупностей|, що мають нормальний розподіл або що мало відрізняється від нього.
Таблиця 21 – Нормальний розподіл накопичених частот (загальний|спільний| об'єм|обсяг| сукупності =10000)
| τ | Р(τ) | τ | Р(τ) | τ | Р(τ) | τ | Р(τ) |
| 0,0 | |||||||
| 0,10 | 1,10 | 2,10 | 3,10 | ||||
| 0,20 | 1,20 | 2,20 | 3,20 | ||||
| 0,30 | 1,30 | 2,30 | 3,30 | ||||
| 0,40 | 1,40 | 2,40 | 3,40 | ||||
| 0,50 | 1,50 | 2,50 | 3,50 | ||||
| 0,60 | 1,60 | 2,60 | 3,60 | ||||
| 0,70 | 1,70 | 2,70 | 3,70 | ||||
| 0,80 | 1,80 | 2,80 | 3,80 | ||||
| 0,90 | 1,90 | 2,90 | 3,90 | ||||
| 1,00 | 2,00 | 3,00 |
Примітка|тлумачення|. У графах Р(τ) нуль цілих для скорочення об'єму|обсягу| опущений.
Приклад|зразок| 3. Індивідуальний відбір з|із| популяції за якою-небудь|будь-якою| ознакою можна проводити, керуючись одним з наступних|слідуючих| принципів:
1) відібрати індивідууми, яким властиві певні значенням ознаки відбору;
2) відібрати індивідууми, що перевищують середнє значення ознаки з|із| певним ступенем|мірою| упевненості.
3) відібрати певну кількість індивідуумів виходячи з можливостей|спроможностей| подальшого|дальшого| вивчення.
Ці задачі селекціонер вирішує, керуючись головним чином своїми знаннями характеру|вдачі| мінливості ознаки, враховуючи особливості умов зростання, які можуть у значній мірі|значною мірою| зсунути в той або інший бік межі випадкових коливань, властиві популяції для «середніх» умов. При цьому застосування|вживання| статистичних методів для виділення кращих родоначальників має допоміжний характер|вдачу|. Проте|тим не менше| ці методи можуть надати істотну|суттєву| допомогу селекціонеру при відборах на хімічний склад, якість продукції та інші ознаки, приховані від ока.
Припустимо, що селекціонер відібрав 2000 кошиків соняшнику; у насінні кожного з них визначено вміст|вміст,утримання| жиру у перерахунку на абсолютно суху речовину. Середня для всієї сукупності олійність складає 46,6 %, середнє квадратичне відхилення – 2,0 %, розмах варіювання – 42,4–53,1 %.
1-е завдання|задача|. Для подальшої|дальшої| роботи передбачається|припускається| відібрати рослини (кошики) з|із| олійністю вище 49 %, або на 2,4 % більше середньої величини. Необхідно з'ясувати: а) вірогідність|ймовірність| того, що ці рослини істотно|суттєво| відрізняються за олійністю від середнього рівня популяції і б) яка кількість рослин з|із| такою олійністю міститься|утримується| (або очікується) в даній сукупності.
Для відповіді на перше питання визначаємо нормоване відхилення τ=(49,0–46,6):2=1,2. Звертаючись|обертаючись| до табл. 21, знаходимо|находимо|, що цьому значенню відповідає накопичена частота 0,3849. Помножуючи|множивши| це число на 2, одержимо|отримаємо| Р=0,770. Якщо така вірогідність|ймовірність| ствердження про перевагу матеріалу, що відібрано не задовольняє дослідника, він повинен виділяти рослини з|із| вищою олійністю.
Для відповіді на друге питання пригадаємо, що 50 % членів вибірки мають значення ознаки вище за середню. Оскільки|тому що| олійність від 46,6 до 49 % мають 38,49 % рослин, то з|із| олійністю вище 49 % їх буде 50–38,49=11,51 %, або 230 з|із| двох тисяч.
2-е завдання|задача|. Необхідно відібрати рослини, що перевищують за олійністю середній рівень з|із| вірогідністю|ймовірністю| Р=0,95|. Згідно табл. 21, цій вірогідності|ймовірності| відповідає х=1,96. Отже, кращі (у цьому розумінні) рослини повинні мати олійність більше, ніж  +xs = 46,6+1,96·2,0=50,5 %. Для того, щоб дізнатися|упізнати,взнати,пізнати|, скільки може бути в даній сукупності рослин з|із| такою олійністю, обчислюємо|обчисляємо,вичисляємо| τ=(50,5–46,6):2=1,95 і за табл. 19 знаходимо|находимо| відповідь: 50,00–47,42=2,58 %, або небагато чим|мало чим| більше 50 рослин.
+xs = 46,6+1,96·2,0=50,5 %. Для того, щоб дізнатися|упізнати,взнати,пізнати|, скільки може бути в даній сукупності рослин з|із| такою олійністю, обчислюємо|обчисляємо,вичисляємо| τ=(50,5–46,6):2=1,95 і за табл. 19 знаходимо|находимо| відповідь: 50,00–47,42=2,58 %, або небагато чим|мало чим| більше 50 рослин.
3-е завдання|задача|. Для вивчення в селекційному розпліднику 1-го року потрібно відібрати 300 рослин, тобто|цебто| 15 % від загального|спільного| їх числа. Необхідно з'ясувати, яку олійність повинні мати рослини, що відібрані. За умовами завдання|задачі| підлягає вибраковуванню 85 %, з|із| них 50 % мають показники олійності нижче, а 35 % – вище за середню арифметичну. Звертаючись|обертаючись| до табл. 21, знаходимо|находимо|, що 35 % накопичених частот відповідає τ=1,05. Згідно формулі (3), знаходимо|находимо|, що для виконання поставленої умови треба відібрати рослини з|із| олійністю не менше 48,7 %.
З|із| наведених прикладів|зразків| стає ясним, що середнє квадратичне відхилення дає можливість|спроможність| з|із| відомим ступенем|мірою| точності встановити вірогідність|ймовірність| приналежності будь-якого спостереження до даного варіаційного ряду|лави,низки|. Тому середнє квадратичне відхилення часто називають також середньою помилкою окремих спостережень.






