Рассмотрим n взаимно независимых случайных величин 
, 
, …, 
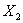, которые имеют одинаковые распределения, и следовательно, одинаковые характеристики (математическое ожидание М, дисперсию D, среднее квадратическое отклонение s. Введем новую случайную величину — среднее арифметическое рассматриваемых величин 
:
и изучим числовые характеристики .
Математическое ожидание среднего арифметического одинаково распределенных взаимно независимых случайных величин равно математическому ожиданию каждой из этих величин:
М( )=М.
Дисперсия среднего арифметического n одинаково распределенных взаимно независимых случайных величин в n раз меньше дисперсии каждой из этих величин:
D( )=D/n.
Среднее квадратическое отклонение среднего арифметического n одинаково распределенных взаимно независимых случайных величин в 
раз меньше среднего квадратического отклонения каждой из этих величин:
s( )=s/ .
Таким образом, среднее арифметическое достаточно большого числа взаимно независимых случайных величин имеет значительно меньшее рассеяние, чем каждая отдельная величина. С увеличением n величина почти перестает быть случайной и приближается к постоянной М. Тем самым оправдывается рекомендуемый в практической деятельности способ получения более точных результатов измерений: одна и та же величина измеряется многократно, и в качестве ее значения берется среднее арифметическое полученных результатов измерений.
