Можно привести пример двух дискретных случайных величин Х и Y, которые имеют различные возможные значения и при этом одинаковые математические ожидания. Рассмотрим следующие ряды распределения Х и Y:
| X | -100 | Y | -1 | |||
| p | 0,5 | 0,5 | p | 0,5 | 0,5 |
Математические ожидания величин Х и Y равны друг другу:
M[X] = -100×0,5+100×0,5 = -50+50 = 0
M[Y] = -1×0,5+1×0,5 = -0,5+0,5 = 0
Возможные значения величин Х и Y значительно отличаются. Таким образом, зная лишь математическое ожидание случайной величины, нельзя судить ни о ее возможных значениях, ни о рассеянии значений около математического ожидания.
Зададимся вопросом, как можно задать величину разброса возможных значений величины. На практике эта величина чрезвычайно важна. Например, ее необходимо знать, оценивая кучность поражения мишени при стрельбе из пистолета. На первый взгляд, кажется, что необходимо проанализировать отклонение случайной величины от M[X].
Отклонением называют разность между случайной величиной и ее математическим ожиданием: Х –М[Х].
Однако оказывается, что математическое ожидание отклонения случайной величины равно 0:
М[Х – М[Х]]=0.
Действительно, М[Х – М[Х]]= М[Х] – M[М[Х]]= М[Х] – M[Х]=0.
Это объясняется тем, что одни отклонения положительны, а другие – отрицательны. И в результате их взаимного сложения значение отклонение будет равно 0. Поэтому отклонение случайной величины нельзя использовать для оценки ее рассеяния. Для этого чаще всего вычисляют среднее значение квадрата отклонения, называемое дисперсией.
Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:
D[Х] = М[(Х – М[Х])2]. (6.4)
Рассмотрим дискретную случайную величину Х, принимающую значения  ,
,  , …,
, …,  с вероятностями
с вероятностями  ,
, 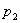 , …,
, …,  . Используя в выражении (6.4) определение математического ожидания (6.3), получим следующую формулу для вычисления дисперсии:
. Используя в выражении (6.4) определение математического ожидания (6.3), получим следующую формулу для вычисления дисперсии:
D[Х] =  =
=
 ×
×  +
+  ×
× 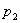 + … +
+ … +  ×
×  . (6.5)
. (6.5)
Для вычисления дисперсии также можно пользоваться следующей формулой:
D[Х] = М[Х2] – (М[Х])2. (6.6)
Докажем формулу (6.6). Раскрыв квадрат разности, получим:
D[Х] = М[(Х – М[Х])2] = М[Х2 – 2×Х×М[Х]+ М[Х]2].
Учитывая, что М[Х] – это некоторое постоянное число, раскроем предыдущее равенство так: D[Х] = М[Х2]–M[2×Х×М[Х]]+M[М[Х]2] = М[Х2]– 2×(М[Х])2 +(М[Х])2 = М[Х2] – (М[Х])2.
Таким образом, D[Х] = М[Х2] – (М[Х])2 =  – (М[Х])2 =
– (М[Х])2 =  ×
×  +
+ 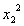 ×
× 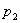 + … +
+ … +  ×
×  – (М[Х])2.
– (М[Х])2.
Пример 6.9. Найти дисперсию случайной величины, ряд распределения которой:
| X | |||
| p | 0,2 | 0,5 | 0,3 |
В примере 6.6 мы подсчитали математическое ожидание этой случайной величины: М[X]=3,2. Теперь вычислим дисперсию. По определению D[X]=(1-3,2)2×0,2 + (3-3,2)2×0,5 + (5-3,2)2×0,3 = (-2,2)2×0,2 + (-0,2)2×0,5 + 1,82×0,3 = 4,84×0,2 + 0,04×0,5 + 3,24×0,3=1,96.
Для нахождения дисперсии можно воспользоваться и формулой (6.6):
D[X]=12×0,2+32×0,5+52×0,3–3,22=1×0,2+9×0,5+25×0,3–10,24=0,2+4,5+7,5–10,24 =1,96.
Как видно из вычислений, 2-й способ – по формуле (6.6) – значительно проще.
Свойства дисперсии случайной величины:
1. Дисперсия постоянной величины равна нулю:
D[C]=0.
2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат:
D[C×Х]=C2×M[X].
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин:
D[Х+Y]=D[X]+D[Y].
4. Дисперсия разности двух независимых случайных величин равна сумме дисперсий этих величин:
D[Х–Y]=D[X]+D[Y].
Пример 6.10. Вычислим дисперсию случайной величины, ряд распределения которой имеет вид (пример 6.1):
| X | ||
| p | 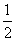
| 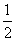
|
Вспомним, что для этой случайной величины M[X]= 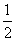 . Используя формулу (6.5), получаем:
. Используя формулу (6.5), получаем:
D[X]=(0– 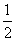 )2×
)2× 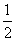 +(1–
+(1– 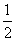 )2×
)2× 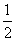 =
= 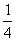 ×
× 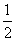 +
+ 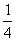 ×
× 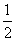 =
= 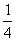 .
.
Рассчитаем дисперсию числа появлений события А в одном испытании, если вероятность этого события равна p. Математическое ожидание Х равно: M[X]= p. Дисперсия случайной величины Х:
D[X]=(0– p)2×(1– p)+(1– p)2× p = p ×(1– p) × (1– p + p)= p ×(1– p).
Рассмотрим случайную величину X – число появления события А в n независимых испытаниях и найдем ее дисперсию. Вероятность появления события А в каждом испытании постоянна. По прежнему будем обозначать ее через p, а вероятность непоявления события А через q =1– p.
Дисперсия D[X] числа появлений события А в n независимых испытаниях, в каждом из которых вероятность p появления события одинакова, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании:
M[X]= npq.
Дисперсия биномиально распределенной случайной величины, рассматриваемой в примере 6.4 (n =3, а p =0,6), равна D[X]= n×p × (1– p)= 3×0,6×0,4=0,72






