Середня зважена є результатом усереднювання середніх арифметичних декількох сукупностей|. Вона обчислюється за формулою (7):
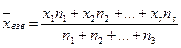(7)
де хвзв| – середня зважена; х1, х2, х3 – середні арифметичні 1-ої, 2-ої і т.д. сукупностей|; n1, n2, n3 – об'єм|обсяг| сукупності.
Приклад|зразок| А. Відомасередня висота і кількість саджанців лавра благородного (Laurus nobilis L.) на трьох карантинних ділянках. Вони складають: на першій –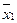 
= 380 мм, n1=1000; на другій – 
= 460 мм n2=500; на третій – 
= 400 мм n3=2000. Потрібно обчислити|обчисляти,вичислити| середню висоту за даними трьох карантинних ділянок.
При обчисленні|підрахунку| середньої зваженої враховують не тільки|не лише| середню висоту рослин на кожні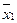й карантинній ділянці (, , ), але й об'єм|обсяг| вибірки (n1, n2, n3), за якою була обчислена|обчисляти,вичислені| середня арифметична на кожній карантинній ділянці.
Використовуючи для обчислення|підрахунку| середньої зваженої формулу (7), одержимо|отримаємо|:
Приклад|зразок| Б. Розрахуйтесередній вміст нітратів в листках рослин чорнобривців розлогих (Tagetes patula L.) в червні, липні і серпні, за наведеними в табл. 12 даними.
Таблиця 12
| Місяці | Середній вміст нітратів в листках, мг/г сухої речовини | Об'єм|обсяг| вибірки |
| Червень | 42,3 | |
| Липень | 50,4 | |
| Серпень | 52,3 |
4. Обчислення|підрахунок| середнього квадратичного відхилення. Порівняємо, наприклад, дані з підрахунку кількості стебел|стеблин| у|в,біля| 10 рослин двох сортів|гатунків| ячменю:
| сорт|гатунок| А....... | ||||||||||
| сорт|гатунок| Б....... |
Середня арифметична обох сортів|гатунків| однакова і дорівнює 3-м стеблам|стеблинам|. В той же час неважко|скрутно| помітити|помітити|, що більшість варіант першого сорту має значення, рівне середньому, а інші – близькі до нього; у другого ж сорту є|наявний| варіанти, які різко відрізняються від 
. Інакше кажучи, ознака, що вивчається, у|в,біля| сорту|гатунку| А варіює значно менше, ніж у|в,біля| сорту|гатунку| Б, і в цьому відношенні сорти|гатунки| не тотожні.
Ступінь|міру| варіювання краще всього характеризувати шляхом порівняння значення кожної з варіант із|із| середньою арифметичною. Насправді|дійсно|, якщо всі варіанти вибірки мають значення, що дорівнюють середній арифметичній, то ніякого|жодного| варіювання немає. І, навпаки, чим більше відрізняються значення варіант від середньої і чим істотніше відмінність між окремими варіантами, тим сильніше варіюють варіанти за ознакою|лава,низка|.
Повернемося до прикладу|приміром| варіювання числа стебел|стеблин| у|в,біля| двох сортів|гатунків| ячменю. При обчисленні|обчисляючи,вичисливши| відхилення значення кожної з варіант від середньої арифметичної, одержимо|отримаємо| такі| два ряди|лави,низки| цифр:
| сорт|гатунок| А...... | – 1 | – 1 | + 1 | + 1 | ||||||
| сорт|гатунок| Б....... | – 2 | – 2 | – 1 | – 1 | + 1 | + 2 | + 3 |
Варіанти другого ряду|лави,низки| сильніше відхиляються від середньої арифметичної, або, інакше кажучи, розсіяння його більше, ніж розсіяння першого ряду|лави,низки|. Здавалося б, що для характеристики середньої величини відхилень досить було б обчислити|обчисляти,вичислити| їх середнє арифметичне, тобто|цебто| підсумовувати їх і поділити на загальне|спільне| число. Але|та| практично це здійснити неможливо, оскільки|тому що| сума відхилень від завжди дорівнює нулю.
Для характеристики ступеня|міри| варіювання відхилення окремих варіант від середньої арифметичної підносять у квадрат. При цьому всі знаки стануть позитивними, і сума їх буде позитивною величиною. Крім того, при піднесенні в квадрат і підсумовуванні відхилень, які як надалі відстоять від середньої, є|з'являються,являються| відносно великими доданками. Внаслідок цього сума квадратів відхилень при одному і тому ж числі спостережень буде тим більше, чим суттєвіше розкид експериментальних даних.
Щоб елімінувати вплив об'єму|обсягу| сукупності, суму квадратів ділять на число спостережень. Одержаний|отриманий| таким чином середній квадрат відхилень від середньої арифметичної називають дисперсією (або розсіянням). Дисперсія генеральної сукупності позначається|значиться| σ2. При обробці вибіркових сукупностей знаходять|находять| оцінку генеральної дисперсії s2, що більш менш наближається до σ2.
Добувши корінь квадратний з|із| σ2, знаходять|находять| показник варіювання, так зване середнє квадратичне відхилення (або стандартне відхилення), яке відіграє дуже важливу|поважну| роль при аналізі дослідних даних.
Таким чином, загальною|спільною| формулою для знаходження s (або σ|β,α³λ|) буде:
(8)
При обробці згрупованих варіаційних рядів|лав,низок| формула (8) набуває такого вигляду:
(9)
де х – значення ознаки, що варіює; – середня арифметична; f – частоти групи; n – загальне|спільне| число спостережень.
Знаменник «n–1» називають у статистиці «числом ступенів свободи». Така назва пояснюється тим, що в статистиці при обчисленні|підрахунку| будь-яких середніх величин використовують число незалежних величин. При обчисленні|підрахунку| середньої арифметичної всі спостереження беруть участь в її утворенні і в цьому відношенні незалежні один від одного. Тому суму значень ділять на загальне|спільне| число, варіант, тобто|цебто| на n. Коли ж обчислюють|обчисляють,вичисляють| середнє відхилення, то число незалежних величин буде не n, а n–1, оскільки|тому що| кожне з відхилень визначається величиною всіх інших і чисельно дорівнює їх сумі, узятих із|із| зворотним знаком. Так, якщо є|наявний| чотири відхилення від середньої: 4, –2, –3, +1, то, наприклад, 4 = (–2) + (–3) +1 = –4 і т.д. Тому суму квадратів відхилень ділять не на n, а на n – 1. Це означає, що (n–1) відхилень є|з'являються,являються| незалежними величинами і можуть мати будь-яке значення, а одне відхилення позбавлено свободи варіювання і визначається іншими. Число мір свободи зазвичай позначають|значать| грецькою буквою|літерою| υ (ню).
У великих вибірках (близько 300–500 і більше варіантів) зменшення дільника дисперсії на одиницю мало змінює|зраджує| його абсолютну величину. Середнє квадратичне відхилення – завжди позитивна величина і виражається|виказується,висловлюється| в тих же одиницях вимірювання|виміру|, що і ознака, що вивчається.
Перш ніж перейти до розгляду різних способів обчислення|підрахунку| середнього квадратичного відхилення, вкажемо, що ∑(х– |)2 може бути обчислена|обчисляти,вичислена| за будь-якою з наступних|слідуючих| формул:
∑(х– |)2= 
або ∑f(х– |)2= 
(10)
∑(х– |)2= 
або ∑f(х– |)2= 
(11)
∑(х– |)2= 
або ∑f(х– |)2= 
(12)
Застосування|вживання| цих формул значно скорочує об'єм|обсяг| обчислювальної роботи, особливо при використанні для розрахунків рахунково-обчислювальних машин.
Приклад|зразок| А. Вичисліть середню арифметичну і середнє квадратичне відхилення за формулою (9) для розподілу даних у табл. 13.
Таблиця 13 – Розподіл емпіричних даних
| Середнє значення групи (Х) | Частоти (f) | fX | fX2 |
| X |
см2
.
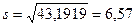Для перевірки вірності обчислення|підрахунку| суми квадратів відхилень слід повторити її обчислення|підрахунок|, застосувавши іншу формулу, наприклад (8).
5. Обчислення|підрахунок| коефіцієнта варіації. Середнє квадратичне відхилення, що якнайкраще характеризує ступінь|міру| мінливості ознаки, є|з'являється,являється| початковою|вихідною| величиною для визначення ряду|лави,низки| інших статистичних показників. Один з них – це так званий коефіцієнт варіації є характеристикою ступеня|міри| варіювання.
В процесі досліджень часто виникає необхідність зіставити міру варіювання однієї і тієї ж ознаки в різних вибірках (наприклад, у|в,біля| різних сортів|гатунків|) або різних ознак у|в,біля| представників однієї вибірки або одного сорту, виду рослин. Проте|однак| безпосередньо за величиною s можна судити про відносну силу варіювання тільки|лише| в тих випадках, коли середні арифметичні обох рядів|лав,низок| дорівнюють одна одній. За різних значень порівняння ступеня|міри| мінливості викликає|спричиняє| утруднення|скруту|. Пояснимо це наступним|таким| прикладом|зразком|. У|в,біля| двох сортів|гатунків| ярової пшениці і s довжини головного стебла|стеблини| дорівнюють: у|в,біля| Гордєїформе 432 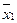= 77,5 см; s1 = 7,50 см; у|в,біля| Гордєїформе 802 = 92,1 см; s2 = 11,6 см.
Середні значно відрізняються одна від одної, і за величиною s важко|скрутно| сказати, у|в,біля| якого з|із| цих сортів|гатунків| сильніше варіює довжина стебла|стеблини|. Ще більше утруднень|скрути| спостерігається при оцінці ступеня|міри| варіювання різних ознак у|в,біля| одного і того ж сорту|гатунку|. Проте|однак| всі вони значною мірою відпадають, якщо для характеристики варіювання скористатися не абсолютним, а відносним значенням середнього квадратичного відхилення, тобто|цебто| відношенням|ставленням| s до , вираженим|виказаним,висловленим| у відсотках|процентах|. Це і буде коефіцієнт варіації (V):
(13)
Так, наприклад, якщо s = 7,50, = 77,5, то для цих даних 
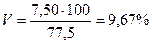, тобто|цебто| середнє квадратичне відхилення складає 9,67 % від середньої арифметичної у|в,біля| сорту|гатунку| Годєїформе 435 і 12,59 % у|в,біля| сорту|гатунку| Гордєїформе 802.
Слід підкреслити, що значення коефіцієнта варіації особливо різко проявляється при порівнянні варіювання декількох ознак між собою. Зіставлення коефіцієнтів варіації дає ясне уявлення про ступінь|міру| варіювання ознак у даному досліді|досліді|.
6. Визначення показника різноманітності для альтернативних ознак. Якщо результати спостережень групуються в протилежні одна одній групи, їх варіювання на відміну від рядової мінливості називається альтернативним, а ознаки, за якими проводять спостереження альтернативними. Наприклад, співставлення чоловічих і жіночих особин|осіб|, хворих і здорових рослин і т.д. Показник різноманітності для альтернативних ознак визначають за допомогою середнього квадратичного відхилення в абсолютних і відносних значеннях за формулою:
або 
(14)
де σ|β,α³λ| – показник різноманітності для альтернативних ознак; p – частка|доля| особин|осіб|, що мають дану ознаку в сукупності; q – частка|доля| особин|осіб|, позбавлених даної ознаки в сукупності.
Приклад|зразок|. З|із| 100 рослин тюльпанів висаджених на клумбі 650 виявилися червоні, а 350 – пістрявопелюсткові (це може бути ознакою вірусного захворювання і бути небажаною ознакою). Визначити величину середнього квадратичного відхилення за показником наявності червоного забарвлення|фарбування| віночка.
; 
; 
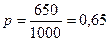p + q = 1
7. Оцінка варіант, що відхиляються. Найбільше значення ознаки у вибірці називається максимальною варіантою|, а найменше – мінімальною варіантою|. Якщо в ранжируваному варіаційному ряді |лаві,низці| значення максимальної або мінімальної варіанти надмірно велике або мале порівняно з сусідніми значеннями ряду|лави,низки|, то необхідно перевірити приналежність до даної сукупності тих варіант, що таких різко відхиляються, оскільки вони можуть відноситися до іншого сорту|гатунку|, іншої популяції, а також виникнути із-за грубої помилки при вимірюванні|вимірі| або підрахунку. У подібних випадках варіанти, що різко відхиляються і чужими для даної сукупності, повинні бути виключені з|із| вибірки. Проте|однак| це виключення|виняток| повинно бути обґрунтовано за допомогою кількісної оцінки відхилення таких варіант.
Для максимальної варіанти (за нормального або близькому до нього розподілі варіант) застосовується формула (15):
(15)
де υN – критерій приналежності максимальної варіанти до сукупності; хN – максимальна варіанта; XN–1 – варіанту, наступна|слідуюча| за величиною після максимальної; х2 – варіанта, що стоїть у ранжируваному ряду|лаві,низці| поряд із|поряд із| мінімальною.
Перевіримо, наприклад, приналежність варіанти 82 в табл. 14 до даної сукупності.
Таблиця 14 – Висота рослин сої (у см) у вигляді ранжируваного незваженого варіаційного ряду|лави,низки|
| Варіанти |
| ∑х = 839 |
| N = 13 |
.
Оскільки|тому що| обчислене|обчисляти,вичислене| значення критерію, яке для N = 13 дорівнює 0,520 (табл. 15), менше табличного, то варіанту не можна виключати з|із| вибірки.
Таблиця 15 – Значення критеріїв υN і υ1 при рівнях значущості 0,01 (верхнє число) і 0,05 (нижнє число)*
| N | ΥN(1) | N | ΥN(1) | N | ΥN(1) |
| 0,991 0,955 | 0,520 0,410 | 0,414 0,320 | |||
| 0,916 0,807 | 0,502 0,395 | 0,407 0,314 | |||
| 0,805 0,689 | 0,486 0,381 | 0,400 0,309 | |||
| 0,740 0,610 | 0,472 0,369 | 0,394 0,304 | |||
| 0,683 0,554 | 0,460 0,359 | 0,389 0,299 | |||
| 0,635 0,512 | 0,449 0,349 | 0,383 0,295 | |||
| 0,597 0,477 | 0,439 0,341 | 0,378 0,291 | |||
| 0,566 0,450 | 0,430 0,334 | 0,374 0,287 | |||
| 0,541 0,428 | 0,421 0,327 | 0,369 0,283 |
* Якщо обчислені|обчисляти,вичислені| значення υN або υ1 перевищують табличні, то варіанта відкидається
Для мінімальної варіанти при розподілі, що не сильно відрізняється від нормального, застосовується формула:
(16)
υ1 – критерій приналежності мінімальної варіанти х1 до сукупності; х2 – варіанта, що стоїть поряд із|поряд із| мінімальною; ХN–1 – друга за значенням варіанта після|потім| максимальної.
Для прикладу|зразка| оцінимо приналежність варіанти 43 у табл. 14 до даної сукупності:
.
Розраховане значення критерію менше за табличне (табл. 15): 0,029 < 0,520, тому відкидати варіанту не можна|прямує|.
У випадку, якщо|у разі, якщо,в случае | різко відхиляються за величиною не тільки|не лише| крайні варіанти, але й сусідні з|із| ними, приналежність їх до даної сукупності оцінюється за тими ж формулами. Наприклад, з|із| варіаційного ряду|лави,низки| 192, 187, 135, 127, 120, 111, 98, 87, 71, 66, 52, 47, 41, 12, 9 треба перевірити варіанту 187 і варіанту 12. Якщо ці варіанти виявляться чужими для даної вибірки, то варіанти 192 і 9 також повинні бути виключені. Якщо відомо середнє квадратичне відхилення нормально розподіленої сукупності, то оцінку ступеня|міри| відхилення максимальної або мінімальної варіанти можна зробити точніше за допомогою табл. 15 і формул (17) і (18):
(17)
(18)
де σ|β,α³λ| – середнє квадратичне відхилення, решта позначень такі ж, що і у формулах (15) і (16).
Якщо відомо значення σ|β,α³λ| (σ|β,α³λ| = 11,98) повторимо процедуру оцінки цих же варіант за формулами (17) і (18).
.
За табл. 16 критичне значення для об'єму|обсягу| сукупності N = 10 (приймаємо найближче менше число) при рівні значущості 0,05 дорівнює 1,46, що більше обчислювальних значень. Отже, немає підстав відкидати як максимальну, так і мінімальну варіанти. Якщо варіанта після|потім| описаних способів перевірки відкидається, то обчислення|підрахунок| σ|β,α³λ| слід повторити для нової зменшеної вибірки.
Таблиця 16 – Критичне значення різниці між двома крайніми варіантами сукупності
| Об'єм|обсяг| сукупності, N | Рівні значущості | Об'єм|обсяг| сукупності, N | Рівні значущості | ||||||
| 0,10 | 0,05 | 0,01 | 0,005 | 0,10 | 0,05 | 0,01 | 0,005 | ||
| 2,33 | 2,77 | 3,64 | 3,97 | 0,83 | 1,04 | 1,50 | 1,70 | ||
| 1,79 | 2,17 | 2,90 | 3,20 | 0,82 | 1,03 | 1,50 | 1,67 | ||
| 1,18 | 1,46 | 2,03 | 2,27 | 0,81 | 1,02 | 1,47 | 1,57 | ||
| 1,03 | 1,27 | 1,80 | 2,00 | 0,75 | 0,95 | 1,38 | 1,55 | ||
| 0,96 | 1,20 | 1,70 | 1,90 | 0,72 | 0,91 | 1,32 | 1,50 | ||
| 0,91 | 1,15 | 1,63 | 1,85 | 0,70 | 0,88 | 1,30 | 1,47 | ||
| 0,88 | 1,11 | 1,60 | 1,80 | 0,68 | 0,87 | 1,28 | 1,45 | ||
| 0,86 | 1,08 | 1,57 | 1,76 | 0,65 | 0,83 | 1,22 | 1,40 | ||
| 0,84 | 1,06 | 1,53 | 1,72 |
