Розглянутий вище прямий метод обчислення|підрахунку|  за умов наявності великої кількості варіант досить трудоємний. При обчисленні|підрахунку| середньої арифметичної великої вибірки користуються непрямим методом. Наведемо приклад|зразок| обчислення|підрахунку| середньої арифметичної способом здобутків|добутків|, при якому використовують варіаційні ряди|лави,низки|. Розрахунок проводиться|виробляється,справляється| за формулою (6):
за умов наявності великої кількості варіант досить трудоємний. При обчисленні|підрахунку| середньої арифметичної великої вибірки користуються непрямим методом. Наведемо приклад|зразок| обчислення|підрахунку| середньої арифметичної способом здобутків|добутків|, при якому використовують варіаційні ряди|лави,низки|. Розрахунок проводиться|виробляється,справляється| за формулою (6):
 ;
; 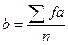 або
або  (6)
(6)
де А – довільно вибирана умовна середня; b – поправка, яку потрібно додати до А для отримання|здобуття|  .
.
Приклад|зразок|. Визначити середню площу|майдани| листкової|аркуша| пластинки платана східного (Plathanus orientalis L.) за даними табл. 11. При розв’язуванні завдання|задавання| необхідно вибрати умовну середню (А). зазвичай за таку приймають значення середини того класу, до якого входить найбільше число варіант. У нашому випадку А = 21 см2. Щоб за допомогою середньої величини обчислити|обчисляти,вичислити| середню арифметичну потрібно знайти поправку (b). Для цього в третій графі табл. 11 відзначають, на скільки класових проміжків відхиляється від умовної середньої середина кожного класу. Ці відхилення позначаються|значаться| буквою|літерою| а.
Таблиця 11 – Обчислення|підрахунок| середньої площі|майдану| листкової поверхні платана східного (Plathanus orientalis L.), см2
| Серединне значення класу (W) | Частота (f) | Відхилення (а) | Здобуток відхилення на частоту (fa) | Сума здобутків відхилень на частоту (fa) |
| – 4 | – 12 | – 65 | ||
| – 3 | – 18 | |||
| – 2 | – 20 | |||
| – 1 | – 15 | |||
| + 1 | + 19 | + 78 | ||
| + 2 | + 28 | |||
| + 3 | + 18 | |||
| + 4 | + 8 | |||
| + 5 | + 5 | |||
| Сума | + 13 | + 13 |
Починати|розпочинати,зачинати| треба з класу, середина якого становить 21. Його відхилення від умовної середньої (А = 21) дорівнює нулю. Клас 19 відхиляється на один класовий проміжок, клас 17 – на 2, клас 15 – на 3, клас 13 – на 4 проміжки. Відхилення цих класів мають негативний знак|заперечні|, оскільки їх значення менше умовної середньої. Класи 23, 25, 27, 29 і 31 відхиляються від умовної середньої теж|також| на 1, 2, 3 і т.д. класових проміжків, але|та| їх відхилення позитивні, оскільки варіанти в них більше умовної середньої. Записавши відхилення з|із| їх знаками в третю графу таблиці, помножують відхилення кожного класу (а) на відповідну частоту (f) і здобуток (fa) вписують у четверту графу таблиці. Потім підсумовують всі значення fa з урахуванням|з врахуванням| їх знаку, спочатку всі позитивні (+fa), потім всі негативні|заперечні| (–fa), і відраховують з|із| більшої суми меншу, зберігаючи знак більшої величини.
У нашому випадку сума позитивних значень fа рівна +78, сума негативних|заперечних| –65. Їх сума дорівнює (+78) + (–65) = +13. Суму fa вписують у нижній рядок п'ятої графи. Здобуток fa є вираженою в числі класових інтервалів сумою відхилень варіант від умовної середньої. У нашому прикладі вона не дорівнює 0. Отже, для обчислення середньої арифметичної потрібно знайти величину поправки (b):

Додавши до умовної середньої поправку, одержують|отримують| середню арифметичну:  = А + b = 21 + 0,26 = 21,26 см2.
= А + b = 21 + 0,26 = 21,26 см2.






