≤. “еоретична частина|частка|. ѕеред початком роботи сл≥д ознайомитись з|≥з| терм≥нами ≥ р≥зними способами угрупуванн€ первинних результат≥в спостережень, пон€тт€ми про статистичн≥ таблиц≥ та вар≥ац≥йн≥ р€ди|лави,низки|.
1. ѕон€тт€ про генеральну сукупн≥сть, велику ≥ малу виб≥рки. ћетоди б≥ометр≥њ заснован≥ на теор≥њ в≥рог≥дност≥|ймов≥рност≥| ≥ теор≥њ помилок. ѕрипустимо|передбачимо|, що попул€ц≥€ рослин, що ц≥кавить нас, складаЇ 1 млн. екземпл€р≥в|прим≥рник≥в|. ¬с≥ екземпл€ри|прим≥рники| категор≥њ, що вивчаЇтьс€, складатимуть генеральну сукупн≥сть. ЌемаЇ н≥€коњ|жодноњ| можливост≥|спроможност≥| (та ≥ необх≥дност≥) вивчити таку численну|багаточисельну| групу методом ц≥лковитого обстеженн€. ” випадках, коли вим≥рюванн€|вим≥р| пов'€зане з видаленн€м рослин з|≥з| субстрату цей метод обстеженн€ недоц≥льний|ц≥лком|. “ому дл€ вивченн€ властивостей або ознак генеральноњ сукупност≥ в≥дбирають частину|частку| рослин, тобто складають виб≥рку.
ўоб виб≥рка повн≥стю в≥дображала|в≥дображувала| генеральну сукупн≥сть, вона повинна бути в≥рно складена. ƒл€ цього у виб≥рку сл≥д в≥д≥брати в однаков≥й к≥лькост≥ ≥ пропорц≥йно генеральноњ сукупност≥ особини|ос≥б| з|≥з| малими, середн≥ми ≥ високими значенн€ми ознаки, що вивчаЇтьс€, або властивост≥, що практично теж|також| неможливо зробити. “ому в≥дб≥р ≥з|≥з| генеральноњ сукупност≥ проводитьс€ за принципом випадковост≥. ¬≥рог≥дн≥сть|ймов≥рн≥сть| попаданн€ у виб≥рку т≥Їњ або ≥ншоњ особини|особи| з|≥з| генеральноњ сукупност≥ випадков≥. ≤снуЇ таблиц€ випадкових чисел за €кою можна в≥д≥брати рослини уникаючи упередженост≥. ќтже, що при вивченн≥ генеральноњ сукупност≥ за виб≥ркою, тобто характеристиц≥ ц≥лого за його частиною|частц≥|, ≥ випадковому в≥дбор≥ у виб≥рку з|≥з| генеральноњ сукупност≥ неминуча помилка.
ќб'Їм|обс€г| генеральноњ сукупност≥ може бути €к дуже великим, так ≥ дуже малим. Ќаприклад, сорт|гатунок| плодових дерев, за €ким оц≥нюЇтьс€ врожайн≥сть, вже Ї генеральною сукупн≥стю. ƒл€ визначенн€ середньоњ врожайност≥ у саду генеральною сукупн≥стю будуть вс≥ дерева в саду. оли об'Їм|обс€г| генеральноњ сукупност≥ дуже великий, то вона прир≥внюЇтьс€ до неск≥нченност≥. “аким чином, генеральною називають сукупн≥сть, €ка м≥стить|утримуЇ| у соб≥ ≥нформац≥ю, необх≥дну дл€ вир≥шенн€ певного завданн€|задач≥|. ¬иб≥рки складають ≥з урахуванн€м|з врахуванн€м| вс≥х особливостей рослин: виду|виду|, сорту|гатунку|, в≥ку, умов вирощуванн€ та ≥н. ѕри цьому можлив≥ р≥зноман≥тн≥ випадков≥ поЇднанн€ чинник≥в|фактор≥в|, що позитивно ≥ негативно|заперечний| впливають на ознаку та обумовлюють|зумовлюють| њњ р≥зноман≥тн≥сть. Ѕ≥ометр≥€ ≥ вивчаЇ випадков≥ €вища, €к≥ в сукупност≥ ви€вл€ють певн≥ законом≥рност≥.
ƒуже важливим|поважним| питанн€м Ї|з'€вл€Їтьс€,€вл€Їтьс€| чисельн≥сть виб≥рки. ¬изначенн€ чисельност≥ виб≥рки залежить в≥д характеру|вдач≥| питань, що вивчаютьс€, ступен€|м≥ри| њх вивченост≥ та ≥нших умов. „исло особин|ос≥б| у виб≥рц≥ позначаЇтьс€|значитьс€| буквою|л≥терою| n, а в генеральн≥й сукупност≥ N. –озр≥зн€ють велик≥ ≥ мал≥ виб≥рки, а у зв'€зку з цим ≥ неоднаков≥ методи обробки показник≥в ознак. ¬еликими називають виб≥рки, чисельн≥сть особин|ос≥б| в €ких складаЇ 30 ≥ б≥льше, малими Ц виб≥рки з|≥з| чисельн≥стю особин|ос≥б| менше 30.
|
|
|
2. ѕравила побудови|шикуванн€| статистичних таблиць. ѕервинн≥ спостереженн€, одержан≥|отриман≥| в результат≥|унасл≥док,внасл≥док| реЇстрац≥њ (вим≥рюванн€|вим≥р|, п≥драхунок) значень ознаки, що вар≥юЇ, не дозвол€ють у б≥льшост≥ випадк≥в шл€хом безпосереднього огл€ду ви€вити €к≥-небудь законом≥рност≥ або характеристики сукупност≥ в ц≥лому|загалом|. ¬ той же час систематизован≥, зведен≥ в таблиц≥ дан≥ спостережень часто дають наочне|нагл€дне| у€вленн€ про характер|вдачу| м≥нливост≥ даноњ ознаки ≥ дозвол€ють значно спростити техн≥ку обчисленн€|п≥драхунку| р≥зних статистичних показник≥в.
якщо внасл≥док спостережень одержано|отримано| невелику к≥льк≥сть вар≥ант (близько 10Ц20), то дл€ наочност≥|нагл€дност≥| ≥ подальшоњ|наступноњ| статистичний обробки њх сл≥д розташувати в певн≥й посл≥довност≥|лад≥|, наприклад за убуванн€м або зростанн€м значень ознаки, що вар≥юЇ. “ака систематизац≥€ називаЇтьс€ ранжируванн€м, а р€д|лава,низка| Ц ранжируваним.
ѕри великому числ≥ спостережень систематизац≥€ зводитьс€ до складанн€ статистичноњ таблиц≥. —татистичн≥ таблиц≥ бувають р≥зного вигл€ду|виду|. онструкц≥€ њх залежить в≥д того, €к≥ особливост≥ сукупност≥ належить досл≥джувати. ¬они можуть включати дан≥, що характеризують розпод≥л член≥в сукупност≥ за одним або дек≥лькома незалежними або взаЇмозв'€заними ознаками, в статиц≥ або в динам≥ц≥ ≥ т.п. “абл. 1Ц7 дають у€вленн€ про основн≥ типи елементарних статистичних таблиць.
“аблиц€ 1 Ц –озпод≥л 500 колос≥в озимоњ пшениц≥ сорту|гатунку| Ѕ≥лоцерк≥вська 198 за вагою нас≥нн€ (безперервне вар≥юванн€)
| ¬ага нас≥нн€ 1 колоса (у м≥л≥грамах, в≥д Ц до) | |||||||||||
| 401Ц500 | 501Ц600 | 601Ц700 | 701Ц800 | 801Ц900 | 901Ц1000 | 1001Ц110 | 1101Ц1200 | 1201Ц1300 | 1301Ц1400 | 1401Ц1500 | –азом |
јналог≥чний вигл€д|вид| маЇ таблиц€ розпод≥лу при дискретному вар≥юванн≥.
“аблиц€ 2 Ц –озпод≥л 500 колос≥в озимоњ пшениц≥ сорту|гатунку| Ѕ≥лоцерк≥вська 198 за к≥льк≥стю плодючих|плодючих,пл≥дних| колоск≥в
| „исло колоск≥в в колос≥ | |||||||||||
| –азом | |||||||||||
–озпод≥ли €к≥сних ознак найчаст≥ше характеризують у вигл€д≥ табл. 3 дл€ дек≥лькох або табл. 4 Ц дл€ двох ознак (альтернативне вар≥юванн€). “ак≥ таблиц≥ називають Д таблиц€ми контингентност≥| (складу) Ф.
“аблиц€ 3 Ц –озпод≥л рослин другого покол≥нн€ г≥брид≥в озимоњ пшениц≥ за типом колосу
| «абарвленн€|фарбуванн€| червоне | «абарвленн€|фарбуванн€| б≥ле | –азом | ¬сього колос≥в | |||||
| остист≥ | безост≥ | остист≥ | безост≥ | червоних | б≥лих | остистих | безостих | |
“аблиц€ 4 Ц –озпод≥л нас≥нн€ кукурудзи за забарвленн€м|фарбуванню| ендосперму
| Ѕ≥ле | ∆овте | ¬сього |
ќсобливим видом статистичних таблиць Ї так звана корел€ц≥йна таблиц€ (Д корел€ц≥йна реш≥тка Ф), що характеризуЇ розпод≥л член≥в сукупност≥ одночасно за двома ознаками (табл. 5).
|
|
|
“аблиц€ 5 Ц –озпод≥л 100 колос≥в €чменю за довжиною ≥ числом зерен у них (корел€ц≥йна таблиц€)
| „исло зерен в колос≥ | ƒовжина колоса (у см) | |||||||
| 12Ц14 | 15Ц7 | 18Ц20 | 21Ц23 | 24Ц26 | 27Ц29 | 30Ц32 | сума | |
| —ума |
Ќеважко|скрутно| в≥дм≥тити|пом≥тити|, що п≥дсумки дають розпод≥л одних ≥ тих же 100 колос≥в: вертикальний Ц за числом зерен у колос≥, а горизонтальний Ц за довжиною колоса.
ѕри альтернативному вар≥юванн≥ таблиц€ под≥бного типа маЇ назву Ђтаблиц≥ спр€женост≥ї або Ђчотирьохкл≥тинноњ|кл≥тковоњ|ї (2×2) (табл. 6).
“аблиц€ 6 Ц –озпод≥л нас≥нн€ кукурудзи за польовою схож≥стю залежно в≥д способу п≥дготовки пос≥вного матер≥алу
| —пос≥б п≥дготовки нас≥нн€ | „исло нас≥нн€ | –азом | |
| схожого | несхожого | ||
| «вичайний|звичний|........................... | |||
| «агартовуванн€ при знижен≥й температур≥........ | |||
| –азом................................... |
“аблиц≥, що показують зм≥ну €коњ-небудь ознаки у|в,б≥л€| представник≥в одн≥Їњ ≥ т≥Їњ ж сукупност≥ за певн≥ пром≥жки часу, тобто|цебто| в динам≥ц≥, називають хронолог≥чними (табл. 7).
“аблиц€ 7 Ц ƒовжина стебла|стеблини| рослин кукурудзи сорту|гатунку| ¬оронежська 76 за декадами, см
| ƒата спостережень | |||||
| 18/V≤ | 28/V≤ | 8/V≤≤ | 18/V≤≤ | 28/V≤≤ | 7/V≤≤≤ |
—татистичн≥й обробц≥ часто п≥дл€гають ≥ складн≥ш≥ таблиц≥, в €ких з≥ставл€Їтьс€|сп≥вставл€Їтьс€| вар≥юванн€ одн≥Їњ ≥ т≥Їњ ж ознаки у|в,б≥л€| р≥зних сукупностей|, наприклад таблиц≥ даних врожайност≥ сорт≥в|гатунк≥в| у сортовипробуванн≥| й т.п.
3. ѕравила побудови|шикуванн€| вар≥ац≥йних р€д≥в|лав,низок|. ѕриступаючи до побудови|шикуванн€| вар≥ац≥йного р€ду|лави,низки| потр≥бно в сукупност≥ початкових|вих≥дних| даних в≥дшукати л≥м≥ти Ц м≥н≥мальну (xmin) ≥ максимальну (xmax) вар≥анти. Ћ≥м≥ти вказують|вказують| на загальний|сп≥льний| розмах р≥зноман≥тност≥ ознак. ѕот≥м використовуючи формулу визначити величину класового ≥нтервалу λ (л€мбда).
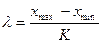 (1)
(1)
де λ Ц розм≥ри класового ≥нтервалу; xmin ≥ xmax Ц м≥н≥мальн≥ ≥ максимальн≥ значенн€ вар≥ант сукупност≥; Ц к≥льк≥сть клас≥в, на €к≥ сл≥д розбити вар≥ац≥ю ознаки. ≥льк≥сть клас≥в можна визначити за табл. 8.
“аблиц€ 8 Ц ≥льк≥сть клас≥в дл€ певного числа спостережень
| „исло спостережень n (в≥д Ц до) | ≥льк≥сть клас≥в, |
| 25Ц40 40Ц60 60Ц100 100Ц200 >200 | 5Ц6 6Ц8 7Ц10 8Ц12 10Ц15 |
“очн≥ше число клас≥в визначаЇтьс€ так: = 1 + 3,32 lg n. якщо сукупн≥сть дуже велика (n >100) можна використовувати формулу = 5 lg n.
якщо зТ€суЇтьс€|, що λ=1, з≥браний матер≥ал розпод≥л€Їтьс€ в без≥нтервальний| вар≥ац≥йний р€д|лаву,низку|; €кщо ж λ не дор≥внюЇ одиниц≥, вих≥дн≥ дан≥ необх≥дно розпод≥лити в ≥нтервальний р€д|лаву,низку|. ѕри цьому точн≥сть розм≥ру класового ≥нтервалу повинна в≥дпов≥дати точност≥, прийн€т≥й при вим≥рюванн≥|вим≥р≥| ознаки. Ќаприклад, к≥льк≥сть кв≥ток на рослинах г≥б≥скуса| (n = 60) вар≥юЇ в≥д 3,21 до 4,55 шт. ” такому раз≥|в такому раз≥| класовий ≥нтервал встановлюЇтьс€ таким чином:
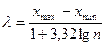 (2)
(2)
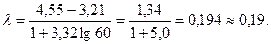
ѕрийн€то округл€ти|округлювати| дл€ зручност≥ величину класового ≥нтервалу. “аке округленн€ може впливати на к≥льк≥сть клас≥в: при зб≥льшенн≥ величини класового пром≥жку к≥льк≥сть клас≥в може зменшуватис€, а при њњ зменшенн≥ Ц зб≥льшуватис€. якщо точн≥сть вим≥рюванн€|вим≥ру| даноњ ознаки обмежити дес€тими|дес€теро| дол€ми одиниц≥, розм≥р класового ≥нтервалу опинитьс€ наступний|сл≥дуюча|:

” обох випадках результати спостережень повинн≥ розпод≥л€тис€ в ≥нтервальний вар≥ац≥йний р€д|лаву,низку|.
|
|
|
ѕри побудов≥|шикуванн≥| ≥нтервального вар≥ац≥йного р€ду|лави,низки| сл≥д поступати|надходити| так, щоб м≥н≥мальна вар≥анта сукупност≥ потрапл€ла|попадала| приблизно в середину першого класового ≥нтервалу. ¬иконанн€ ц≥Їњ вимоги гарантуЇ побудову|шикуванн€| вар≥ац≥йного р€ду|лави,низки|, €кий найб≥льш повно в≥дпов≥даЇ природ≥ €вища, що вивчаЇтьс€, а отже, ≥ найменш≥ втрати ≥нформац≥њ про точн≥сть обчислюваних|обчисл€ти,вичисл€ти| статистичних характеристик р€ду|лави,низки|. ÷≥й вимоз≥ задовольн€Ї формула (3):
хн| = хmin Ц λ/2 (3)
де хн| Ц нижн€ межа|кордон| першого класового ≥нтервалу; хmin Ц м≥н≥мальна вар≥анта досл≥джуваноњ сукупност≥; λ Ц розм≥ри класового ≥нтервалу.
“ак, при хmin = 3,21 ≥ λ = 0,19 нижн€ межа|кордон| першого класу дор≥внюЇ хн| = 3,21Ц0,19/2 = 3,115.
Ќам≥тивши класов≥ ≥нтервали, залишаЇтьс€ розпод≥лити за ними вс≥ вар≥анти сукупност≥, тобто визначити частоти кожного класу. ѕроте|однак| тут виникаЇ питанн€: у €к≥ класи в≥дносити вар≥анти, €к≥ за своЇю величиною сп≥впадають|зб≥гаютьс€| з|≥з| верхньою межею|кордоном| одного ≥ нижньою межею|кордоном| ≥ншого, сус≥днього класу? Ќаприклад, в €кий клас сл≥д в≥днести вар≥анту 3,31 Ц в перший або в друг≥й? ÷е питанн€ розв'€зуЇтьс€|вир≥шуЇтьс€| по-р≥зному. ћожна пом≥щати в один ≥ той же клас вар≥анти, €к≥ б≥льше нижньоњ, але|та| менше або р≥вн≥ його верхн≥й меж≥|кордону|, тобто за принципом Ђв≥д ≥ до включної. „аст≥ше поступають|надход€ть| таким чином: верхн≥ меж≥|кордони| клас≥в зменшують на величину, р≥вну точност≥, що прийн€та при вим≥рюванн≥|вим≥р≥| ознаки, чим ≥ дос€гаЇтьс€ необх≥дне розмежуванн€ клас≥в. ўоб вар≥анта не потрапл€ла|попадала| на межу|кордон| м≥ж двома класами умовно позначають|значать| до €кого класу в≥дноситьс€ сум≥жна величина. « ц≥Їю метою зменшують верхню межу|кордон| кожного класу на величину р≥вну 0,1 (0,01) точност≥ вим≥рюванн€|вим≥ру| ознаки (табл. 9).
“аблиц€ 9 Ц —татистична таблиц€ до перетворенн€ ≥ п≥сл€ перетворенн€
| ¬ага плоду суниц≥, г | —ередина клас≥в | |
| ѕеред перетворенн€м | ѕ≥сл€|пот≥м| перетворенн€ | |
| 12,0Ц14,0 | 12,0Ц13,9 | |
| 14,0Ц16,0 | 14,0Ц15,9 | |
| 16,0Ц18,0 | 16,0Ц17,9 | |
| 18,0Ц20,0 | 18,0Ц19,9 | |
| 20,0Ц22,0 | 20,0Ц21,9 | |
| 22,0Ц24,0 | 22,0Ц23,9 | |
| 24,0Ц26,0 | 24,0Ц25,9 |
Ќаступний|такий| крок веде до зам≥ни класових ≥нтервал≥в на њх центральн≥ або серединн≥ значенн€. ¬ результат≥ ≥нтервальний вар≥ац≥йний р€д|лава,низка| перетворюЇтьс€ на без≥нтервальний| р€д|лаву,низку|. Ќеобх≥дн≥сть такоњ зам≥ни повТ€зана з тим, що числов≥ характеристики, що узагальнюють (середн€, дисперс≥€ та ≥н.) обчислюютьс€|обчисл€ютьс€,вичисл€ють| за без≥нтервальними| р€дами|лавах,низках|. —ерединн≥ значенн€ класових ≥нтервал≥в (х≥), €к це вит≥каЇ з формули хн| = хmin Ц λ/2, в≥дсто€ть в≥д њх нижн≥х меж|кордон≥в| хн| на величину, що дор≥внюЇ половин≥ класового ≥нтервалу.
Ќайточн≥ше центральну величину класового ≥нтервалу можна одержати|отримати| за формулою:
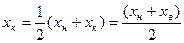 (4)
(4)
де хк| Ц к≥нцева|ск≥нченна| точка ≥нтервалу, що дор≥внюЇ початку наступного|такого| класу, зменшеному на точн≥сть вим≥рюванн€|вим≥ру| ознаки.
—ередини клас≥в набувають значенн€ окремих вар≥ант ≥ називаютьс€ класовими вар≥антами на в≥дм≥ну в≥д конкретних вар≥ант, що складають дану сукупн≥сть. ќписану методику можна продемонструвати на прикладах|зразках|.
ѕриклад|зразок| 1. Ќа клумб≥ зареЇстровано 64 рослини сальв≥њ| блискучоњ|лискучоњ|. ≥льк≥сть кв≥ток на кожн≥й кв≥тц≥, вар≥ювало таким чином:
|
|
|
” ц≥й сукупност≥ хmin = 5 ≥ хmах = 12. «в≥дси

ќск≥льки|тому що| ознака вар≥юЇ дискретно ≥ λ=1, сукупн≥сть спостережень сл≥д розпод≥лити в без≥нтервальний| вар≥ац≥йний р€д|лаву,низку|, тобто безпосередньо за ранжируваними значенн€ми ознаки, €к≥ ≥ будуть класами даного р€ду|лави,низки|.
ўоб при визначенн≥ частот кожного класу не збитис€ з рахунку|л≥чби|, потр≥бно побудувати|спорудити| допом≥жну (розрахункову) таблицю, в €к≥й перша графа заповнюЇтьс€ класами (у даному випадку ранжируваними значенн€ми ознаки), а друга необх≥дна дл€ обл≥ку|урахуванн€| частот fi, що розпод≥л€ютьс€ за цими класами.
–ознесенн€ частот за класами провод€ть|виробл€ють,справл€ють| таким чином. ѕрогл€даючи сукупн≥сть результат≥в спостережень, в друг≥й граф≥ розрахунковоњ таблиц≥ за допомогою умовних знак≥в в≥дзначають повторюван≥сть вар≥ант дл€ кожного класу. ѕри цьому рекомендуЇтьс€ не вишукувати однаков≥ вар≥анти, а розносити њх за класами, що не одне ≥ те ж. «неважанн€|нехтуванн€| ц≥Їњ рекомендац≥њ призводить|призводить,наводить| до помилок, зайвих витрат|затрат≥| прац≥ ≥ часу на виконанн€ роботи. ”мовними знаками при рознесенн≥ результат≥в спостережень за класами можуть бути крапки|точки|, риски та ≥нш≥ знаки. «ручним, особливо при обробц≥ великих сукупн  остей|, ви€вл€Їтьс€|опин€Їтьс€| наступний|сл≥дуючий| шифр частот:
остей|, ви€вл€Їтьс€|опин€Їтьс€| наступний|сл≥дуючий| шифр частот:

|
| 1 2 3 4 5 6 7 8 9 10 |
якнайкращим|щонайкращим,найкращим| способом рознесенн€ вар≥ант Ї|з'€вл€Їтьс€,€вл€Їтьс€| розкладанн€ бланк≥в, кожний з €ких в≥дпов≥даЇ окремому спостереженню ≥ м≥стить|утримуЇ| значенн€ ознак. ” цьому випадку значенн€ ознаки, що потрапл€ють|попадають| до одного класу р€ду|лави,низки|, утворюють окрему купку бланк≥в. ¬сього таких купок опинитьс€ ст≥льки, ск≥льки утворено ≥нтервал≥в вар≥ац≥йного р€ду|лави,низки|. ѕ≥сл€|пот≥м| зак≥нченн€ рознесенн€ њњ результати можна неодноразово перев≥рити п≥драхуванн€м кожноњ ≥з купок бланк≥в, тобто прогл€данн€м тих вар≥ант, €к≥ потрапили|попали| до кожного класу р€ду|лави,низки|. ÷е дозвол€Ї повн≥стю виключити помилки, можлив≥ при ≥нших способах п≥драхунку класових частот.
«ак≥нчивши рознесенн€ вар≥ант за класами, перевод€ть|перекладають,переказують| шифр частот у числа. ¬ результат≥ отримують третю графу допом≥жноњ таблиц≥, що м≥стить|утримуЇ| частоти без≥нтервального| вар≥ац≥йного р€ду|лави,низки| (табл. 9).
ќдержаний|отриманий| вар≥ац≥йний р€д|лава,низка| в≥дбиваЇ залежн≥сть м≥ж окремими вар≥антами та њх зустр≥чаЇмост≥ в дан≥й сукупност≥, тобто законом≥рн≥сть вар≥юванн€ ознаки, що досл≥джуЇтьс€.
4. ѕобудова|шикуванн€| граф≥к≥в вар≥ац≥йних р€д≥в|лав,низок|. ƒл€ того, щоб наочн≥ше|нагл€дн≥ше| у€вити законом≥рн≥сть вар≥юванн€ к≥льк≥сних ознак, вар≥ац≥йн≥ р€ди|лави,низки| прийн€то зображувати|змальовувати| у вигл€д≥ граф≥к≥в. “ак, при побудов≥|шикуванн≥| граф≥ка без≥нтервального| вар≥ац≥йного р€ду|лави,низки| по ос≥ абсцис в≥дкладають серединн≥ значенн€ клас≥в, по ос≥ ординат Ц частоти (табл. 10). ¬исота перпендикул€р≥в, що опускають на в≥сь абсцис, в≥дпов≥даЇ частотам клас≥в. ѕри зТЇднуванн≥ верх≥вок перпендикул€р≥в пр€мими л≥н≥€ми, одержують|отримують| геометричну ф≥гуру у вигл€д≥ багатокутника, €ка називаЇтьс€ пол≥гоном розпод≥лу частот. Ћ≥н≥€, що зТЇднуЇ верх≥вки перпендикул€р≥в, називаЇтьс€ вар≥ац≥йною кривою або кривою розпод≥лу частот вар≥ац≥йного р€ду |лави,низки| (рис. 1).
“аблиц€ 10
| ласи х≥ | Ўифр частот | „астоти р≥ |

| ||

| ||

| ||

| ||

| ||

| ||
| ||

| ||
| —ума |
ѕри побудов≥|шикуванн≥| граф≥ка ≥нтервального вар≥ац≥йного р€ду|лави,низки| по ос≥ абсцис в≥дкладають меж≥|кордони| класових ≥нтервал≥в, по ос≥ ординат Ц частоти ≥нтервал≥в. як результат виходить так звана г≥стограма розпод≥лу частот. Ќа рис. 2 зображена|змальована| г≥стограма розпод≥лу вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ сорту|гатунку| Ѕезоста. якщо з|≥з| середин верхн≥х стор≥н пр€мокутник≥в г≥стограми опустити перпендикул€ри на в≥сь абсцис, г≥стограма перетворюЇтьс€ на пол≥гон розпод≥лу, а л≥н≥€, що обТЇднуЇ|поЇднуЇ,з'ЇднуЇ| середини верхн≥х стор≥н пр€мокутник≥в г≥стограми, буде вар≥ац≥йною кривою.
|
|
|
 –ис. 1. ѕол≥гон розпод≥лу чисельност≥ кв≥ток на 64 рослинах, що зростають на клумб≥
–ис. 1. ѕол≥гон розпод≥лу чисельност≥ кв≥ток на 64 рослинах, що зростають на клумб≥
|
 –ис. 2. √≥стограма розпод≥лу вм≥сту б≥лка (мг/г сухоњ речовини) в клейковин≥ пшениц≥ сорту Ѕезоста
–ис. 2. √≥стограма розпод≥лу вм≥сту б≥лка (мг/г сухоњ речовини) в клейковин≥ пшениц≥ сорту Ѕезоста
|
якщо по ос≥ абсцис в≥дкладати значенн€ клас≥в, а по ос≥ ординат Ц накопичен≥ частоти з|≥з| подальшим|наступним| обТЇднанн€м крапок|точок| пр€мими л≥н≥€ми, виходить граф≥к, що називаЇтьс€ кумул€тою|. Ќа рис. 3 зображена|змальована| кумул€та| розпод≥ли вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ сорту|гатунку| Ѕезоста. Ќа в≥дм≥ну в≥д вар≥ац≥йноњ кривоњ, що маЇ куполопод≥бну форму, кумул€та| маЇ вид S-образноњ кривоњ. Ќакопичен≥ частоти знаход€ть|наход€ть| посл≥довним п≥дсумовуванн€м, або кумул€ц≥Їю (в≥д лат. сumulatio Ц зб≥льшенн€, скупченн€) частот у напр€мку|направленн≥| в≥д першого класу до к≥нц€ вар≥ац≥йного р€ду|лави,низки|. ¬ даному випадку частоти р€ду|лави,низки| розпод≥лу вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ кумульован≥| таким чином:
„астоти fi................................ 2 6 15 23 25 17 7 5
умул€ти частот Sfi................. 2 8 23 46 71 88 95 100
¬≥дкладаючи по ос≥ абсцис частоти, а по ос≥ ординат Ц значенн€ клас≥в з|≥з| подальшим|наступним| зТЇднанн€м геометричних крапок|точок| пр€мими л≥н≥€ми, €к це показано на рис. 4, одержують|отримують| л≥н≥йний граф≥к, званий ог≥вою.
ѕор≥вн€но з емп≥ричними вар≥ац≥йними кривими, €к≥ мають вигл€д ламаних л≥н≥й, кумул€та| ≥ ог≥ва мають б≥льш обт≥чну форму. ÷€ особлив≥сть дозвол€Ї у р€д≥ випадк≥в в≥ддавати перевагу цим граф≥кам перед емп≥ричною вар≥ац≥йною кривою. ÷ентральна точка кумул€ти| сп≥впадаЇ|зб≥гаЇтьс€| з|≥з| центром розпод≥лу сукупност≥. ÷е даЇ можлив≥сть|спроможн≥сть| використовувати њњ при визначенн≥, наприклад, середн≥х доз б≥олог≥чно активних речовин, що викликають|спричин€ють| позитивний ефект у|в,б≥л€| 50 % п≥ддосл≥дних ≥ндив≥д≥в. ќг≥ва дозвол€Ї пор≥внювати один з|≥з| одним одночасно дек≥лька емп≥ричних розпод≥л≥в нер≥вного об'Їму|обс€гу|.
—л≥д в≥дм≥тити|пом≥тити|, що невм≥ла побудова|шикуванн€| граф≥к≥в призводить до того, що останн≥ виход€ть або у вигл€д≥ гостроверх≥вкових| геометричних ф≥гур з|≥з| вузькою основою|основою,заснуванн€м|, або плосковерх≥вковими|, надм≥рно розт€гнутими по ос≥ абсцис. ” обох випадках граф≥ки погано ос€жн≥, неч≥тко в≥дображають|в≥дображують| законом≥рн≥сть вар≥юванн€.
  –ис. 3. ќг≥ва розпод≥лу вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ сорту|гатунку| Ѕезоста
–ис. 3. ќг≥ва розпод≥лу вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ сорту|гатунку| Ѕезоста
| 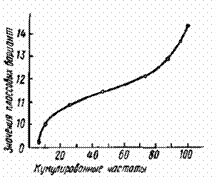 –ис. 4. умул€та розпод≥лу вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ сорту|гатунку| Ѕезоста |справити|
–ис. 4. умул€та розпод≥лу вм≥сту|вм≥сту,утриманн€| б≥лка в клейковин≥ пшениц≥ сорту|гатунку| Ѕезоста |справити|
|
”никнути цих недол≥к≥в|нестач| дозвол€Ї правило Ђзолотого перетинуї, зг≥дно €кому основа геометричноњ ф≥гури повинна в≥дноситис€ до њњ висоти, €к 1:0,62. ѕри побудов≥ вар≥ац≥йноњ кривоњ масштаби на ос€х пр€мокутних координат сл≥д вибирати з|≥з| таким розрахунком, щоб основа кривоњ була в 1,5Ц2,0 рази б≥льше за њњ висоту (тобто максимальноњ ординати). ¬≥дкладаючи по ос≥ абсцис класи вар≥ац≥йного р€ду|лави,низки|, сл≥д також доводити крайн≥ з|≥з| них до нульових клас≥в, в €ких не м≥ститьс€|утримуЇтьс€| жодноњ вар≥анти. ¬ результат≥|унасл≥док,внасл≥док| вар≥ац≥йн≥й крив≥й надаЇтьс€ зак≥нчений, добре ос€жний вигл€д|вид|.






