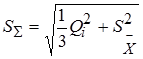Задача суммирования погрешностей заключается в определении расчетным путем оценки результирующей погрешности по оценкам ее составляющих. Если погрешность результата полностью определяется только СИП в виде предельной погрешности СИ, то задачи решается простым суммированием этих погрешностей. Однако, на практике организовать такие измерения практически невозможно. В результатах измерений практически всегда присутствует как СИП так и СЛ, отдельные составляющие погрешности также могут иметь корреляционные связи между собой. Коррелированными являются такие погрешности, которые вызваны одной общей причиной (изменение температуры, влажности, напряжения в сети, магнитными полями, вибрациями и т.д.).
Суммирование СЛ. Суммирование СЛП, как случайной величины производится в зависимости от степени взаимосвязи составляющих случайной суммарной погрешности. Если взаимосвязь между ними отсутствует, (коэффициент корреляции r = 0), то используется геометрическое суммирование: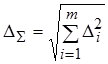 
эта формула обычно дает заниженное значение суммарной погрешности.
Если корреляционная связь между присутствует, коэффициент считается приближенно =1 (коэффициент корреляции r» ±1), то используется арифметическое суммирование: 
эта формула обычно дает завышенное значение суммарной погрешности.
Действительное значение коэффициента корреляции по модулю находится в пределах от 0 до 1. Следовательно действительное значение находится между геометрическим и арифметическим суммированием.
При суммировании составляющих с нормальным законом распределения доверительный интервал может быть найден по формулам:
где Si – оценка СКО i -й составляющей погрешности, m - число суммируемых составляющих погрешности. Знак + следует использовать при расчете составляющих с положительной корреляцией, а - с отрицательной.
При использовании коэффициент Стьюдента при расчете доверительного интервала на уровне доверительной вероятности 0,9 - 0,95 приближенно равен 2.
Суммирование СИП. При определение границ СИП арифметическое их суммирование приводит к существенному завышению результатов, так как формула предполагает проявление этих погрешностей с их максимальным значением что на практике маловероятно. Учитывая, что СИП в какой-то степени определяются случайными причинами, в расчетах используется поправочный коэффициент, зависящий от доверительной вероятности и числа суммируемых составляющих m. qi – граница i - ой составляющей СП.
k = 0,95 - 1,4
При большом числе слагаемых (> 5) доверительный интервал определяется по формуле: 
Суммирование СИП и СЛ. По ГОСТ 8.207 - 76 погрешность результата измерения определяется по следующим правилам:
1. Если оценка СКО результата измерения связана с неисключенной составляющей СИП соотношением: q < 0,8 
, то СИП можно пренебречь и учитывать только СЛ.
2. Если имеет место неравенство: q < 0,8 , то следует пренебречь СЛ, и учитывать только СИП.
Из 1 и 2 следует, что имеет место интервал 0,8 ¸ 8. При невыполнении указанных неравенств границы погрешности результата измерения следует находить по формулам:
; 
