Вероятность безотказной работы - это вероятность того, что в пределах заданной наработки отказ объекта не возникнет. Вероятность безотказной работы определяется в предположении, что в начальный момент времени (момент начала исчисления наработки) объект находился в работоспособном состоянии.
Обозначим через t время или суммарную наработку объекта (в дальнейшем для краткости называем t просто наработкой). Возникновение первого отказа - случайное событие, а наработка τ от начального момента до возникновения этого события - случайная величина. Вероятность безотказной работы P(t) объекта в интервале наработки от 0 до t включительно определяют как
 (3.1)
(3.1)
Здесь Ρ { τ > t } - вероятность события, заключенного в скобках. Вероятность безотказной работы Ρ(t) является функцией наработки t. Обычно эту функцию предполагают непрерывной и дифференцируемой.
Если способность объекта выполнять заданные функции характеризуется одним параметром х, то вместо (3.1) имеем формулу
P (t) = Ρ { х ниж(t1) <х (t 1) < х верх(t 1)}; 0 < t 1£ t, (3.2)
где х ниж(t 1)и х верх(t 1)- предельные по условиям работоспособности значения параметров (эти значения, вообще, могут изменяться во времени). Аналогично вводят вероятность безотказной работы в более общем случае, когда состояние объекта характеризуется набором параметров с допустимой по условиям работоспособности областью значений этих параметров [14].
Вероятность безотказной работы P (t) связана с функцией распределения F (t) и плотностью распределения f (t) наработки до отказа:
F (t) = 1 - P (t); f (t) = dF (t) / dt = - dP (t) / dt. (3.3)
Наряду с понятием «вероятность безотказной работы» часто используют понятие «вероятность отказа» Q (t), то есть вероятность того, что объект откажет хотя бы один раз в течение заданной наработки, будучи работоспособным в начальный момент времени:
Q (t) = 1 - P (t) = F (t). (3.4)
Из (3.3) с учётом (3.4) получим:
 (3.5)
(3.5)
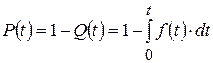 . (3.6)
. (3.6)
 Плотность распределения f (t) наработки до отказа в литературе по надёжности называют частотой отказов, хотя в стандарте этот термин отсутствует. Типичная зависимость частоты отказов f от времени (от наработки) t изображена на рисунке 3.1.
Плотность распределения f (t) наработки до отказа в литературе по надёжности называют частотой отказов, хотя в стандарте этот термин отсутствует. Типичная зависимость частоты отказов f от времени (от наработки) t изображена на рисунке 3.1.
Из неё видно, что всё время работы изделий можно разделить на три участка, соответствующие трём независимым группам отказов. Временной промежуток от 0 до t 1 называется участком приработки. На нем происходят отказы, в основном, из-за дефектов производства. На самом протяжённом основном временном промежутке от t 1 до t 2 выход изделий из строя обусловлен, в основном, внезапными отказами. Временной промежуток от t 2 до t 3 характеризуется возрастанием частоты отказов из-за деградационных процессов, ухудшающих состояние с точки зрения безотказности (старение и износ изделий). На участке после времени t 3 частота отказов уменьшается из-за уменьшения количества исправных изделий. В сложной системе на стадии эксплуатации наряду с деградационными процессами действуют и стабилизирующие процессы, обеспечивающие сопротивление развитию деградации, поддерживающие работоспособность устройства или системы в заданных пределах или восстанавливающие, парирующие ухудшение состояния. К стабилизирующим процессам относятся такие, как автоматическая подстройка и регулировка состояния РЭС при функциональном использовании (автоматическая регулировка усиления - АРУ, автоподстройка частоты - АПЧ и др.), а для восстанавливаемых изделий также подстройки, регулировки, замены на этапах технического обслуживания и ремонта (если отказ всё-таки произошел) [3].
Точечные статистические оценки для вероятности безотказной работы P стат(t), вероятности отказа Q стат(t) и частоты отказов f стат(t) для наработки от 0 до t даются формулами:
P стат(t) =1 - n (t) / N, (3.7)
Q стат(t) = n (t) / N, (3.8)
f стат(t) = n (∆t) / (N×∆t), где (3.9)
N – число объектов, работоспособных в начальный момент времени (наработки); ∆t - промежуток времени (наработки); n (∆t) - число объектов, отказавших в интервале времени (наработки)от t - ∆t / 2 до t + ∆t / 2; n (t) - число объектов, отказавших на отрезке от 0 до t.
Для получения достоверных оценок объем выборки N должен быть достаточно велик [10, 14].






