Операции в АЛУ на двоичными числами с плавающей точкой

 

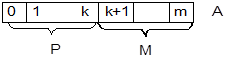
Р – порядок

М – мантисса

 

А=М*2^Р

Если Р определяет диапазон представления чисел в ЭВМ, то М – точность представления чисел в ЭВМ.

 

С:=АqВ; qÎ{+,-,*,/}

 

Необходимое оборудование:

N+2 разряд в мантиссах необходим для округления, т.к. выполнение операций с плавающей точкой связаны с потерей точности.

 

Операнды (ОП) поступают из памяти в ОА в нормализованном виде; знаковые разряды дублируются только на ОЭ. Результат операции тоже должен быть в нормализованном виде.

Нормализованное число: 1/2£|М|<1.

Нормализованное число – это число, у которого первая информационная цифра мантиссы равна 1 для положительных чисел и равна 0 – для отрицательных чисел, и знаковые разряды мантиссы при этом одинаковые.

0 0,1 1001 – нормализованное число

1 1,0 011 – нормализованное число

 

Требования для нормализованных чисел:

М_с(0)ÅМ_с(2)=1

М_с(0)ÅМ_с(1)=0.

 

Виды нарушения нормализации:

1. Нарушение нормализации влево(переполнение мантиссы).

01,110

01 – для положительных чисел

10 – для отрицательных чисел

Восстановление нормализации в этом случае происходит сдвигом мантиссы на один разряд, при этом мантисса уменьшается в два раза, поэтому порядок нужно увеличивать на 1.

 

2. Нарушение нормализации вправо(знаковые разряды мантиссы равны, но не выполняется условие: М_с(0)ÅМ_с(2)=1).

00.00010

11.110

Восстановление нормализации возможно сдвигом мантиссы влево и уменьшением порядка на 1.

 

-1/2₁₀=11,100₂ – нормализованное число, не выполняется условие М_с(0)ÅМ_с(2)=1;

+1/2₁₀=00,100₂

 

Исключительные ситуации при нормализации и после выполнения операций с плавающей точкой.

1. Аварийное завершение операции(прерывание).

Мантисса=0, а порядок любой. Ситуация такая называется потеря значимости.

F_пз:=1; Р:=0.

 

2. При нарушении нормализации влево, после сдвига мантиссы вправо может возникнуть переполнение порядка. Такая ситуация называется переполнение порядка.

F_пп :=1.

 

3. При нарушении нормализации вправо, после сдвига мантиссы влево может возникнуть отрицательное переполнение порядка. Такая ситуация называется исчезновением порядка.

F_ип :=1.

 

Микропрограмма нормализации чисел:

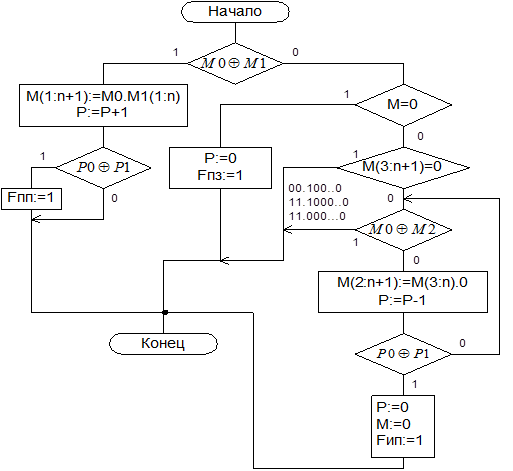
Алгоритм сложения чисел с плавающей точкой.

Даны:

А=М_А*2^Ра

В=М_В*2^Рв

Найти:

С=М_С*2^Рс

Операнды и результат должны быть в нормализованном виде.

 

1. Проверка особых ситуаций:

Если М_В=0, то С:=А

Если М_А=0, то С:=В

Переход к концу.

 

1. Выравнивание порядков.

0,5*10³+0,4*10²=0,5*10³+0,04*10³=0,54*10³.

Вычисление разности порядков: Р_С:=Р_А-Р_В.

Если |Р_С|³n+1, то сумма принимается равной числу с большим порядком:

Если Р_С=0, то С:=А;

Если Р_С=1, то С:=В.

Переход к концу.

Если Р_С¹0, то производится уравнивание порядков слагаемых, путем приведения числа с меньшим порядком к числу с большим порядком. Уравнивание порядков выполняется арифметическим сдвигом мантиссы числа с меньшим порядком вправо на число разрядов равное |Р_С|.

Если ЗнР_с=1, то преобразуется М_А.

Если ЗнР_с=0, то преобразуется М_В.

Сдвиг осуществляется следующим образом:

При каждом элементарном сдвиге на 1 разряд из Р_С вычитается 1, если сдвигается М_В, и прибавляется 1, если сдвигается М_А.

Выход из цикла по Р_С=0.

Если М_А и М_В представлены в прямом коде, то старшие освобождающиеся при сдвиге информационные разряды заполняются нулями; если в инверсном коде, то знаковыми разрядами.

1. Мантиссы, полученные после уравнивания порядков, складываются как числа с фиксированной точкой.

М_С:=М_А+М_В.

Порядок суммы принимается равным наибольшему из порядков слагаемого.

Р_С:=max(Р_А½Р_В).

Отличие от алгоритма сложения с фиксированной точкой – не вырабатывается сигнал переполнения, т.к. возможна нормализация со сдвигом вправо.

 

1. Округление мантиссы результата осуществляется прибавлением 1 к n+2 разряду сумматора мантисс.
2. Нормализация результата (см. алгоритм выше).

 

Исключительные ситуации при сложении:

· Потеря значимости;

· Переполнение порядка при нормализации со сдвигом вправо;

· Исчезновение порядка при нормализации со сдвигом влево.

 

Умножение чисел с плавающей точкой.

С=А*В

Даны:

Р_А, М_А, Р_В, М_В.

Найти:

Р_С, М_С.

1. Порядки складываются по правилам сложения чисел с фиксированной точкой. Мантиссы перемножаются по правилам умножения чисел с фиксированной точкой.
2. Младшие разряды произведения, выдвигаемые в такте сдвига из сумматора мантисс, не сохраняются, кроме n+2 разряда.
3. Результат округляется добавлением 1 в n+2 разряд М_С и нормализуется.

 

Исключительные ситуации:

• Исчезновение порядка при нормализации со сдвигом влево;
• Переполнение порядков, т.к. имеет место сложение порядков в алгоритме.

 

Деление чисел с плавающей точкой.

 

С=А/В.

Р_С=Р_А-Р_В;

М_С=М_А/М_В.

 

Порядки вычитаются, а мантиссы делятся по соответствующим алгоритмам выполнения операций с фиксированной точкой.

 

Исключительные ситуации:

· Деление на ноль;

• Исчезновение порядка при нормализации со сдвигом влево;

· Переполнение порядков, т.к. имеет место сложение порядков в алгоритме.

Особенности применяемого алгоритма деления с фиксированной точкой.

В классический алгоритм деления вносятся незначительные изменения:

· М_А перед выполнением деления с фиксированной точкой сдвигается влево на один разряд, порядок увеличивается на 1.

· Предусматривается нормализация со сдвигом влево.

 

 

Выполнение операций десятичной арифметики в АЛУ.

Не во всех системах команд есть такие операции. Наличие операций десятичной арифметики целесообразно для несложных расчетов коммерческого характера с простыми формулами, где нужны целочисленные вычисления и невыгодно переводить числа в двоичные представления и обратно, для того чтобы над ними выполнить 2-3 операции.

 

Десятичные числа представляются в АЛУ в двоично-десятичном коде.

 

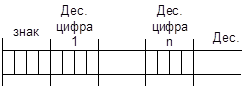
Сложение двух десятичных чисел сводится к последовательной выработке сумм вида:

P_iC_i=A_i+B_i+P_i+1, где

A_i и B_i – четырехразрядные коды десятичных цифр слагаемых;

P_i+1 – десятичный перенос(перенос со сдвигом 10) из предыдущего младшего десятичного разряда суммы;

P_i – десятичный перенос в следующий старший разряд суммы;

C_i – 4-х разрядный двоичный код цифр суммы

A_i+B_i+P_i+1<=19;

 

Построение такой схемы достаточно сложное и схема будет сложной, поэтому обычно для сложения десятичных чисел используется обычный двоичный сумматор, который настраивается на уровне микропрограммы применительно к специфике сложения десятичных чисел.

Вычисление десятичной суммы может быть параллельно-последовательным процессом, т.к. двоичный сумматор имеет ограниченную длину, а число десятичных цифр может варьироваться.

 

Три случая возникающие при сложении десятичных чисел на двоичном сумматоре:

1. 0£C_i£9 C_i

0010+0011=0101

P_i=0

1. 10£C_i£15 C_i

1001+0011=1100

P_i=0

надо: P_i=1, C_i=0010

+

P-1.0010 - C_i

 

1. 16£C_i£19 C_i 0001

1000+1001=0001 +

P_i=1 0110

Если C_i³10, то всегда нужна коррекция.