Синтез формирователей кода (нетиповых ОЭ)

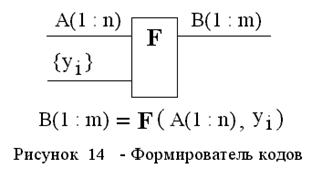
Формирователь кода (ФК) – это нетиповой ОЭ, выполняющий набор микроопераций преобразования входного кода А в выходной код В в соответствии с управляющими сигналами у_i (рисунок 14).

ФК является комбинационной схемой.

Примером ФК является комбинацион­ный счетчик, рассмотренный выше. Он формирует на выходе код, который на 1 больше (меньше) кода на входе. Ши­роко используются также формирова­тели инверсных (обратных и дополни­тельных) кодов, обеспечивающих пра­вильность выполнения операций с от­рицательными числами на двоичном сумматоре [1].

Пример 4. Синтезировать формирователь кодов, выполняющий следующие микрооперации:

- получение модифицированного кода (удвоение знакового разряда), который используется для выявления ситуации переполнения при сложении на двоичном сумматоре чисел с фиксированной точкой;

- удвоение и инвертирование знакового разряда;

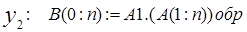- получение модифицированного обратного кода числа;

- сдвиг кода влево без участия двух старших разрядов с доопределением нулем освобождающегося младшего разряда.

Заметим, что значение обратного кода числа с фиксированной точкой А(1:n) определяется значением знакового(старшего) разряда числа – A1. Если число положительное (А1=0), то обратный код числа равен его прямому коду. То же справедливо и для дополнительного кода. Если число отрицательное (А1=1), то для получения обратного кода нужно проинвертировать все разряды числа кроме знакового. Для получения дополнительного кода отрицательного числа нужно к его обратному коду прибавить единицу.

Основной подход при синтезе ФК – выделение и синтез типового разряда.

Этапы синтеза:

1) Выходное слово разбивается на поля однородных разрядов (т.е. разрядов, формируемых одинаково). Для каждого поля значение любого разряда b_i этого поля описывается одной и той же функцией 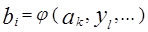. Для указанного примера слово B(1:n) можно разбить на 3 поля:

;

;

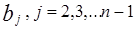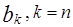(рисунок 15).

2)Синтез типового разряда (построение таблицы выходов). Зависимость значений выходов ФК от значений входного кода и управляющих сигналов представлена в таблице 2.

Таблица 2

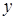
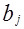
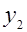
3) Получение выходных функций.

;

;

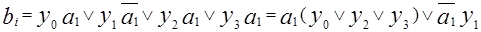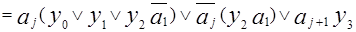Для упрощения функций обычно стараются вынести за скобку прямые и инверсные значения текущего разряда входного кода. Тогда в скобках остаются части, общие для всех выходных разрядов соответствующей группы. Введем следующие обозначения:

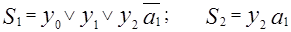
Тогда

;

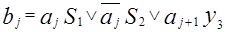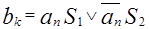
4) Реализация функций, полученных на третьем этапе проектирования. Функциональная схема формирователя кодов, выполненная без привязки к конкретной серии микросхем, представлена на рисунке 16.

При разработке ФК был применен стандартный метод синтеза ОА – синтез типового разряда методами булевой алгебры и дублирования схемы типового разряда для обеспечения требуемой разрядности операционного элемента (ОЭ).

Если набор микроопераций, выполняемых ОЭ, невелик, то его можно скомбинировать из типовых решений, приведенных в справочнике.

Например, нет типового решения для ОЭ, выполняющего микрооперации счета и сдвига. Такой элемент может быть реализован, в частности, путем комбинации типового накапливающего счетчика и типового сдвигающего регистра (рисунок 17,а). Микрооперация сдвига реализуется управляющим сигналом . Операция счета выполняется за три такта как последовательность микроопераций

. Операнд, а затем результат, представлен в регистре, счетчик является вспомогательным элементом. Недостаток схемы: счет осуществляется за три такта. Для преодоления этого недостатка можно предложить схемные решения, изображенные на рисунке 17,б, в.

Примечание - На рисунке 17, не показаны сигналы, инициирующие микрооперации сброса ОЭ и загрузки операнда. В реальной схеме они должны быть предусмотрены.

На рисунке 17,б представлена схема на основе регистра сдвига и комбинационного счетчика. Операнд, а затем результат, находится в регистре. Для исполнения микрооперации сдвига ( ) используется режим сдвига регистра, а для реализации микрооперации счета ( ) – режим параллельной загрузки регистра.

На рисунке 17,в представлена схема на основе накапливающего счетчика и комбинационного сдвигателя. Операнд, а затем результат, находится в счетчике. Для исполнения микрооперации сдвига ( ) используется режим параллельной загрузки счетчика, а для реализации микрооперации счета ( ) – режим счета на увеличение.

Дата добавления: 2015-02-12; просмотров: 450 | Нарушение авторских прав | Изречения для студентов

Читайте также:

ПОЧЕМУ ССОРЫ ПРИЧИНЯЮТ БОЛЬ

Почему человеку так трудно принимать решения

ПОЧЕМУ ЖЕНЩИНЫ НЕ ОБРАЩАЮТСЯ С ПРОСЬБОЙ

Почему необходим контроль?

Рекомендуемый контект:

Поиск на сайте:

© 2015-2020 lektsii.org - Контакты - Последнее добавление