Схема расчета надежности резервированного устройства приведена на рисунке 1. Интенсивности отказов элементов имеют следующие значения:
- l1 = п 1 × 10-4 = 4 × 10-4 1/ч;
- l2 = п 2 × 10-4 = 3 × 10-4 1/ч;
- l3 =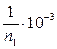 
= 0,25 × 10-3 = 2,5 × 10-4 1/ч;
- l4 =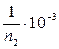 
= 0,33 × 10-3 = 3,3 × 10-4 1/ч;
где п 1 - последняя цифра учебного шифра;
n 2- предпоследняя цифра учебного шифра.
Предполагается, что последействие отказов элементов отсутствует. Необходимо найти среднюю наработку до первого отказа устройства и вероятность его безотказной работы в течение 100 часов.
Решение:
1. Так как готовой формулы для средней наработки до первого отказа в данном случае нет, то необходимо воспользоваться следующем соотношением:
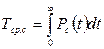
Найдем выражение для вероятности безотказной работы Рс (t)устройства. Очевидно,
Pc(t) = PI(t)× PII(t) × PIII (t)× PIV (t)
В резервированной системе отказ какого-либо элемента не обязательно приводит к отказу всей системы. Типичным случаем является логически параллельное соединение элементов, при котором система отказывает тогда, когда отказывают все ее элементы. Такой тип резервирования называют постоянным. В этом случае все элементы выполняют одну и ту же функцию, работают одновременно и равнонадежны. По теореме умножения вероятностей имеют место следующее выражение:
,
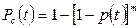где p(t) - вероятности безотказной работы одного элемента.
Тогда:
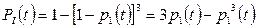
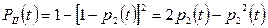
Подставляя значения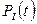 
и 
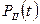в выражение для Pс(t), получим:
- 
- 
+ 
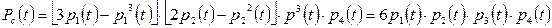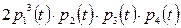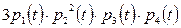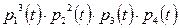
Так как
;
;
;
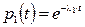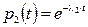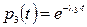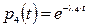, то
- 
- 
+ 
= 
- 
- 
+ 
= 
- 
- 
+ 
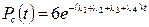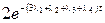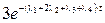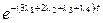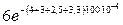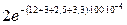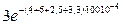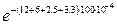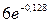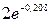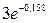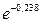= 5,279 – 1,624 – 2,256 + 0,788 = 1,881
2. Определим среднюю наработку до первого отказа
- 
- 
+ 
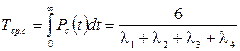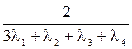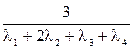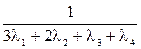
Подставляя в выражение для Тср.с значение интенсивности отказов из условия задачи, получим величину средней наработки до первого отказа.
- 
- 
+ 
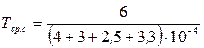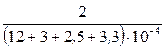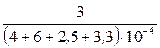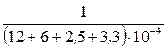= 4687,5 – 961,538 – 1898,734 + 420,168 = 2247,396 ч.
