Количество статистических данных для оценки показателей надежности, полученных в процессе эксплуатации, принципиально ограничено. Полученные по ограниченному объему информации точечные оценки оказываются приближенными, а отклонения этих оценок от значения оцениваемого параметра являются случайными величинами. Необходимо при обработке статистических данных искать более информативные способы оценки параметров по сравнению с точечными оценками. Одним из таких способов является оценка показателей надежности доверительным интервалом. Предположим, что истинное значение средней наработки до отказа - Т 1, а средняя наработка до отказа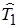 
определена по полученным данным согласно (8.1). Чем меньше число испытаний - N, тем больше расхождение между Т 1 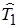и , то есть существует интервал расхождения. Найти точные границы, в пределах которых находится истинное значение искомой величины, не представляется возможным. Однако можно указать двухстороннюю доверительную вероятность 
, которая определяется следующим образом:
, (8.6)
где Т н, Т в – нижняя и верхняя граница доверительного интервала, Т 1 – наработка на отказ.
Доверительный интервал может быть односторонним:
или (8.7)
, (8.8)
где 
, 
- соответствующие односторонние доверительные вероятности событий: Т 1 больше или равна нижней границе доверительного интервала Т н (см. 8.6), Т 1 меньше или равна верхней границе доверительного интервала Т в..
