Надежность ПО или отдельной программы формально можно характеризовать такими же функциональными и числовыми показателями, как и при анализе надежности технических элементов. К основным показателям надежности ПО (или отдельной программы) можно отнести следующие:
- функция ненадежности (риска)
Q(t) = Вер { того, что отказ ПО возникнет до момента t };
- функция надежности
Р(t) = Вер { того, что отказ ПО возникнет после момента t };
- плотность вероятности отказа 
- функция интенсивности отказов
,
являющаяся условной вероятностью возникновения отказа ПО на отрезке (t, t+dt) при условии исправности всех программ до момента t;
- средняя наработка на отказ ПО
.
Основная особенность характеристик надежности ПО заключается в их зависимости от числа ошибок N( 0 ), имеющихся в сертифицированных (сданных в эксплуатацию) программах. Действительно, если программа свободна от ошибок и N( 0 ) = N0 = 0, то Р(τ) 
1 (рис. 4.6).
Рис.4.6 – Зависимость функции надежности ПО от числа ошибок N
При 
>0 и 
> 
вероятность безотказной работы ПО тем быстрее стремится к нулю, чем больше 
по сравнению с , что иллюстрируют графики Р(τ) на рис. 4.6.
Таким образом, функция надежности ПО фактически превращается в семейство распределений 
, зависящих от числа скрытых ошибок N( 0 ) в сертифицированном ПО.
Относительно поведения функции интенсивности отказов во времени τ можно сделать несколько гипотез. Первая из них заключается в том, что 
есть кусочно-постоянная функция с разрывами первого рода в моментах времени 
, j = 1, 2, …, когда проявляется очередная ошибка, возникает отказ программы и после удаления этой ошибки ПО становится надежнее, а уменьшается (см. рис. 4.7, где для простоты показано мгновенное восстановление программ). При этом «ремонтник» не вносит новых дефектов в программу, которая рано или поздно станет абсолютно надежной, а 
.
Рис. 4.7 – Зависимость интенсивности отказа ПО от числа ошибок N
Понятно, что данная гипотеза аналогична первой модели поведения ошибки 
в сертифицированном ПО. Зависимость интенсивности отказов от τ и N описывается формулой:
, 
< 
, j = 1, 2, …,
где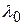 
- параметр; N(0) – число ошибок в ПО при τ = 0; j – порядковый номер обнаруженной ошибки в момент , j = 1, 2, ….
Соответствующая данной гипотезе функция надежности ПО имеет вид:
, < } j = 1, 2, ….
Существуют и другие гипотезы о поведении функции интенсивности 
при переменном числе ошибок в ПО. В частности, предполагается возрастающий кусочно-линейный характер на отрезках 
j = 1, 2, …, где - моменты проявления и мгновенного удаления ошибки (рис. 4.8), или кусочно-линейный ниспадающий вид (рис. 4.9).
Рис. 4.8 - Возрастающая интенсивность Рис. 4.9 – Ниспадающая интенсивность отказа ПО при переменном числе ошибок отказа ПО при убывающем числе ошибок
Следует отметить слабую теоретическую обоснованность всех гипотез о характере функции 
и крайне недостаточное экспериментальное подтверждение их справедливости.
При проектировании АСУ РВ, не имеющих аналогов по программному обеспечению, чаще всего отсутствует какая-либо информация о характере зависимости . Если разрабатываемое ПО достаточно сложное (слабо структурировано, имеет много «опасных» операторов и операций типа прерывание, ввод-вывод, логический переход, взаимные связи с ТСА и т.п.), то в первом приближении на основании второй модели поведения ошибок в ПО допустимо принимать самый «тяжелый» экспоненциальный закон распределения наработки до отказа:
.
Для практических расчетов используется оценка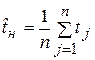 
, где - наработки до отказа тестируемого ПО, n – число отказов ПО на этапе его динамического тестирования.
