Сильная затяжка повышает надежность работы резьбового соединения, так как при этом повышается жесткость стыка и существенно понижается доля переменной нагрузки, приходящейся на болт.
Чтобы обеспечить требуемую затяжку болтов, силу затяжки контролируют. Методы контроля основаны на замере: удлинения болта (шпильки), угла поворота гайки, крутящего момента при затяжке гайки. Первый метод наиболее точен, третий – наиболее распространен вследствие простоты и приспособленности для крупносерийного производства. Контроль в этом случае производят с помощью ключа предельного момента, или динамометрического ключа.
Считается [3], что при затяжке динамометрическим ключом разброс силы затяжки составляет ± (25...30)%, при затяжке на определенный угол поворота гайки – ±15%, при контроле затяжки по деформации тарированной упругой шайбы – ±10%, при контроле удлинения болта – ±(3...5)%. Этим значениям разброса соответствуют приблизительно следующие коэффициенты вариации силы затяжки: 0,09; 0,05; 0,04; 0,02.
Напряжения в болте от внешней нагрузки в затянутом резьбовом соединении определяются с учетом того, что лишь 
- я часть нагрузки передается на болты. Величина , называемая коэффициентом основной нагрузки, может быть оценена расчетом
,
где 
, 
– податливость болта и деталей.
В рабочем диапазоне внешних нагрузок при достаточных силах затяжки болтов для стальных и чугунных деталей обычно =0,2...0,3. Предполагая, что стыки достаточно сильно затянуты и поэтому контактная жесткость мало меняется от давления, до специального изучения рассеяния контактной жесткости можно принимать значение детерминированной величиной. Отсюда коэффициент вариации номинальных напряжений в болте, вызванный рассеянием внешней нагрузки, полагаем равным коэффициенту вариации внешней нагрузки.
Коэффициент концентрации в резьбе в первую очередь определяется формой впадины резьбы. Форма может быть неоговоренной или закругленной.
Для ответственных высоко нагруженных соединений при переменных и динамических нагрузках должна применяться резьба с закругленной впадиной. У этой резьбы радиус кривизны впадины не должен быть менее 0,1 Р, где Р – шаг резьбы. У болтов с закругленной впадиной в конце их обозначений ставят букву R (например, М12 –6g–R), где 6g характеризует степень точности резьбы болта. Рассеяние радиуса впадины заключено в пределах (0,1...0,144) Р независимо [4] от степени точности резьбы.
Эффективный коэффициент концентрации в резьбе определяют экспериментально или через теоретический коэффициент концентрации напряжений и коэффициент чувствительности. Теоретический коэффициент концентрации для наиболее распространенного сопряжения болта с гайкой, работающей на сжатие, связан с шагом Р и радиусом выкружки R зависимостью [*]
Отсюда среднее значение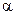 
и коэффициент вариации 
коэффициента концентрации напряжений
;
.
Подготовленный для метрических резьб, применяемых в авиакосмических конструкциях, проект международного стандарта регламентирует радиус впадины в пределах (0,15...0,18) Р. Болты с резьбой, изготовленной по этому стандарту, имеют повышенный предел выносливости. Для этой резьбы 
=3,70 и =0,011.
Вероятностный расчет работоспособности и надежности болтового соединения сводится к оценке вероятности Р безотказной работы соединения, в простейшем предположении равной произведению 
… вероятностей безотказной работы по основным критериям: нераскрытию стыка, несдвигаемости стыка, прочности болтов и т. д. Естественно, что количество учитываемых критериев определяется в зависимости от их значимости.
Вероятность безотказной работы по критерию нераскрытия стыка 
cсоответствует вероятности того, что наименьшее напряжение сжатия в стыке после приложения внешней нагрузки больше нуля.
Для простейшего случая, когда единичное болтовое соединение нагружено центральной отрывающей силой F (величина случайная), вероятность определяют из условия определяют из условия
,
где 
– сила затяжки; 
– множитель, характеризующий долю внешней нагрузки на стык; 
– коэффициент, учитывающий возможное ослабление затяжки вследствие обмятия стыков =1,1. Вероятность 
безотказной работы определяем по табл. в зависимости от квантили
,
где 
– коэффициент запаса нераскрытия стыка по средним нагрузкам
.
Здесь 
и 
средние значения и коэффициенты вариации случайных сил и 
соответственно.
Вероятность безотказной работы по критерию несдвигаемости стыка 
единичного затянутого болтового соединения, нагруженого сдвигающей силой ,
.
Для определения 
вычисляют квантиль 
, (*)
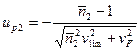где коэффициент запаса несдвигаемости стыка по средним нагрузкам
; 
;
где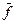 
и 
– среднее значение и коэффициент вариации коэффициента трения 
.
Вероятность безотказной работы по критерию статической прочности
,
где 
– расчетное напряжение в опасном сечении болта, величина случайная.
Расчетное напряжение в болте единичного болтового соединения, нагруженного центральной отрывающей силой, определяется выражением
,
где 
– расчетный диаметр резьбы болта; 
– коэффициент, учитывающий кручение болта (если кручение при затяжке исключено, 
, в остальных случаях 
).
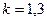Среднее значение расчетного напряжения 
определяем по зависимости для , в которую вместо и подставляем их средние значения 
и 
.
Среднее квадратичное отклонение расчетного напряжения
.
Решая уравнение относительно коэффициента вариации 
, получаем
; 
.
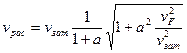Вследствие относительной малости величины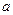 
и соизмеримости коэффициентов вариации 
и 
в технических расчетах принимаем 
.
Вероятность безотказной работы по критерию статической прочности 
находим по квантили
,
где коэффициент запаса прочности по средним напряжениям
,
здесь 
и 
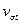– среднее значение и коэффициент вариации предела текучести материала болта.
Вероятность безотказной работы по критерию сопротивления усталости 
, где 
– действующие напряжения, приведенные к симметричному циклу; 
– предел выносливости резьбовой детали (болта).
Среднее значение действующих напряжений определяем по формуле
где – среднее (учитывая случайный характер силы) значение максимальной нагрузки цикла; 0,5 – среднее значение амплитуды нагрузки; 
– коэффициент чувствительности материала к асимметрии цикла; 
– среднее значение эффективного коэффициента концентрации напряжений, принимают в зависимости от предела прочности материала 
, МПа:
| ||||
|
| 3,0 | 3,9 | 4,8 | 5,2 |
или вычисляют по формуле по формуле 
, где 
– коэффициент чувствительности материала к концентрации напряжений, равный 0,5...0,6 для углеродистых и 0,7...0,8 для легированных сталей; 
– среднее значение теоретического коэффициента концентрации напряжений.
Коэффициент вариации напряжения 
можно принимать равным коэффициенту вариации нагрузки , так как влияние на сопротивление усталости средней составляющей напряжений мало по сравнению с переменной.
Среднее значение предела выносливости болта
,
где 
– коэффициент; для соединения стандартными болтами и гайками 
, для соединений типа стяжки 
; 
– коэффициент технологического упрочнения; для болтов с нарезанной резьбой 
, для болтов с накатанной резьбой 
; 
– среднее значение предела выносливости гладкого образца; 
– коэффициент влияния абсолютных размеров.
Коэффициент вариации предела выносливости болта 
включает коэффициенты вариации предела выносливости детали одной плавки, приближенно принимаемого 
или рассчитываемого изложенными выше методами статистического подобия среднего предела выносливости по плавкам, приближённо принимаемого равным 
, и эффективного коэффициента концентрации напряжений 
, и вычисляется по формуле
Вероятность безотказной работы по критерию сопротивления усталости 
определяем в зависимости от квантили нормированного нормального распределения
; 
.
Пример расчета надежности резьбовых соединений приведен в Приложении 2.
