Актуальность исследований и расчета надежности этих соединений вызывается большим рассеянием: натягов, образуемых как разность двух больших близких размеров – диаметров вала и отверстия; коэффициентов трения, зависящих от многих факторов – состояния поверхности, оксидных пленок, случайного попадания масла, а также внешних нагрузок.
Предельный по прочности сцепления момент 
, Н·м, т.е. момент, который может передать соединение диаметром d, мм, длиной l, мм, с натягом N, мкм, при давлении на посадочных поверхностях p, МПа, и коэффициенте трения f, равен
,
где 
– коэффициент, учитывающий возможность уменьшения сил сцепления со временем (от местных обмятий и частичного снятия сил трения).
Для соединения сплошного вала со ступицей с наружным диаметром D, мм, из материалов с одинаковым модулем упругости Е, МПа, и одинаковым коэффициентом поперечного сжатия
,
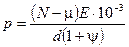где 
; u – поправка на обмятие посадочных поверхностей, зависящая от высоты их микронеровностей 
, 
и принимаемая обычно равной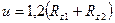 
.
Предельный момент рассматриваем как функцию (произведение) двух случайных величин p и f.
Среднее значение 
предельного момента определяется по средним значениям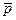 
и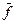 
.
По правилу квадратического сложения коэффициентов вариации аргументов, входящих в выражение функции в виде произведения, находим коэффициент вариации предельного момента
,
где 
– коэффициенты вариации давления и коэффициента трения.
Среднее значение давления 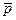вычисляют по вышеприведенной формуле для 
, в которую подставляют среднее значение натяга 
.
Коэффициент вариации давления
,
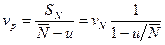где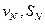 
– коэффициент вариации и среднее квадратическое отклонение натяга.
Если считать поправку на обмятие u пропорциональной натягу N (при малых натягах), то коэффициент вариации давления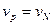 
.
Среднее значение натяга равно разности средних значений отклонений вала 
и отверстия 
, которые в системе отверстия можно выразить через табличные значения допусков диаметров вала 
и нижнее отклонение диаметра вала 
.
Среднее квадратическое отклонение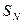 
натяга в обычном предположении, что допуск натяга 
соответствует 
, равно
.
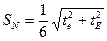Тогда коэффициент вариации натяга 
.
При изготовлении вала и отверстия по одинаковым квалитетам точности, т.е.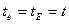 
,
.
Коэффициент вариации коэффициента трения в применении к соединениям с натягом в результате обработки испытаний, проведенных разными исследователями, обычно колеблется в пределах 
(в среднем 0,1). Меньшие значения – при сборке с охлаждением. Самые малые значения, выходящие за указанный интервал, – при гидрозапрессовке (по данным отдельных испытаний). В исследованиях каждого из авторов коэффициенты вариации существенно меньше приведенных выше.
Рассмотрим общую задачу оценке надежности соединения с натягом под действием момента со средним значением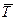 
и коэффициентом вариации 
.
Вероятность 
безотказной работы соединения по критерию прочности сцепления определяем по таблицам нормального распределения в зависимости от квантили 
,
где 
- коэффициент запаса прочности сцепления по средним значениям моментов.
Опасные напряжения возникают у внутренней поверхности охватывающей детали.
Условие прочности 
, где 
наибольшее эквивалентное напряжение; 
- предел текучести материала вариации охватывающей детали.
Среднее значение эквивалентного напряжения 
равно
.
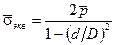Коэффициент вариации 
напряжения равен коэффициенту вариации 
давления на посадочной поверхности соединения. Вероятность безотказной работы 
по критерию прочности деталей определяем в зависимости от квантили
,
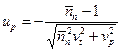где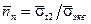 
- коэффициент запаса прочности по средним значениям предела текучести 
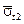и напряжения ; 
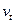- коэффициент вариации предела текучести.
Надежность соединения с натягом, характеризуемую вероятностью безотказной работы Р, определяем как произведение вероятностей 
и 
, т. е. 
.
