Такая система работает не по признакам типа «да – нет», а по конкретным значениям измеренных параметров. При этом не исключено и наличие логических параметров «да – нет», которые, как и в предыдущем случае, заменяют на числовое значение 1(0).
Рассмотрение данного варианта экспертной системы будем вести на том же примере. Тогда параметры, подлежащие замеру, будут выглядеть следующим образом:
Х 1 – разность между показанием датчика температуры 2 и показаниями общего датчика температуры, откорректированного по расходу воды;
Х 2 – разность между показанием датчика температуры 4 и показаниями общего датчика температуры, откорректированного по расходу воды;
Х 3 – разность между показанием водосчетчика 1 и показаниями общего датчика температуры, откорректированного по расходу воды;
Х 4 – разность между показанием водосчетчика 2 и показаниями общего датчика температуры, откорректированного по расходу воды;
Х 5 – разность между показаниями водосчетчиков и общим расходом воды в системе.
Гипотезы Н 1 – Н 4 остаются теми же самыми. Напомним алгоритм выработки правил (рис. 4.56).
Привяжем этот алгоритм к рассматриваемой АСУ ТП. Исходя из опыта эксплуатации систем подобного рода, раздаются начальные значения Хki для всех N гипотез по всем М параметрам, которые и принимаются на первом этапе за средние (Midki), минимальные (xki min) и максимальные (xki max) значения.

Рис. 4.56. Алгоритм выработки правил для системы, принимающей решения
по наименьшему расстоянию
Проводим очередной шаг обучения. Пусть АСУ ТП отказала. Имеем набор показаний  . Вычисляем расстояния D для всех гипотез:
. Вычисляем расстояния D для всех гипотез:
для Н 1:  ; (4.17)
; (4.17)
для Н 2:  ; (4.18)
; (4.18)
для Н 3:  ; (4.19)
; (4.19)
для Н 4:  (4.20)
(4.20)
Нормализация, т.е. деление на максимальный разброс значений, производится для устранения большего влияния бόльших по величине параметров.
После расчетов выбирают гипотезу с наименьшим Dk. Ремонтная бригада приступает к диагностике состояния АСУ ТП и устранению неисправностей, после чего становится известно, была выбрана правильная гипотеза или нет. Какая бы ни была выбрана гипотеза, правильная или неправильная, для гипотезы, соответствующей имевшему место событию, проводится следующая корректировка параметров.
Пусть Nk – число корректировок гипотезы Нk (начальное значение Nk равно 1). Тогда 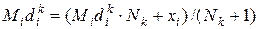 ,
,  .
.
Рассмотрим вышеприведенный алгоритм на примере.
Пусть средние значения на очередном шаге распределились следующим образом.
Н 1 – неисправен водосчетчик 1.
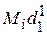 = 5 %;
= 5 %;  = 2 %;
= 2 %;  = 10 %;
= 10 %;
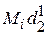 = 0,5 %;
= 0,5 %;  = 0 %;
= 0 %;  = 1 %;
= 1 %;
 = 3 %;
= 3 %;  = 2 %;
= 2 %; 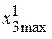 = 5 %;
= 5 %;
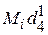 = 0 %;
= 0 %;  = 0 %;
= 0 %;  = 1 %;
= 1 %;
 = 0,6 %;
= 0,6 %;  = 0 %;
= 0 %;  = 1 %.
= 1 %.
Н 2 – неисправен датчик температуры 2.
 = 5 %;
= 5 %;  = 2 %;
= 2 %;  = 10 %;
= 10 %;
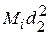 =0,5 %;
=0,5 %;  = 0 %;
= 0 %;  = 1 %;
= 1 %;
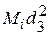 =3 %;
=3 %;  = 2,5 %;
= 2,5 %;  = 5 %;
= 5 %;
 = 0 %;
= 0 %;  = 0 %;
= 0 %;  = 1 %;
= 1 %;
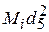 = 4 %;
= 4 %;  = 3 %;
= 3 %; 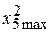 = 7 %.
= 7 %.
Н 3 – неисправен водосчетчик 3.
 = 0,5 %;
= 0,5 %;  = 0 %;
= 0 %;  = 1 %;
= 1 %;
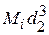 = 5 %;
= 5 %;  = 2 %;
= 2 %;  = 10 %;
= 10 %;
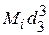 = 0 %;
= 0 %;  = 0 %;
= 0 %;  = 1 %;
= 1 %;
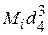 = 3 %;
= 3 %; 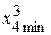 = 2 %;
= 2 %;  = 5 %;
= 5 %;
 = 0,6 %;
= 0,6 %; 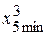 = 0%;
= 0%;  =1%.
=1%.
Н 4 – неисправен датчик температуры 4.
 = 0,5 %;
= 0,5 %;  = 0 %; x41max = 1 %;
= 0 %; x41max = 1 %;
 = 5%;
= 5%; 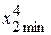 = 2 %;
= 2 %; 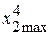 = 10 %;
= 10 %;
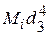 = 0;
= 0; 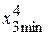 = 0 %;
= 0 %;  = 1 %;
= 1 %;
 = 3 %;
= 3 %;  = 2 %;
= 2 %;  = 5 %;
= 5 %;
 = 4 %;
= 4 %; 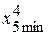 = 2 %;
= 2 %;  = 6 %.
= 6 %.
Предположим, что при очередной неисправности в работе АСУ ТП мы получили следующие замеры: Х 1 = 4 %, Х 2 = 0,2 %, Х 3 = 4 %, Х 4 = 0,1 %, Х 5 = 2 %.
Просчитаем расстояния D для всех четырех гипотез.
Для Н 1: D 1 =  +
+ 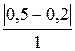 +
+  +
+  +
+  =
=
= 0,125 + 0,3 + 0,33 + 0,1 + 1,4 = 2,225.
Для Н 2: D 2 =  +
+ 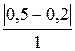 +
+  +
+  +
+  =
=
= 0,125 + 0,3 + 0,4 + 0,1 + 0,5 = 1,425.
Для Н 3: D 3 = 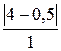 +
+  +
+ 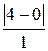 +
+ 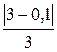 +
+  =
=
= 3,5 + 0,6 + 4 + 0,96 + 1,4 = 10,46.
Для Н 4: D 4 = 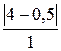 +
+  +
+ 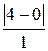 +
+ 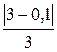 +
+  =
=
= 3,5 + 0,6 + 4 + 0,96 + 0,5 = 9,56.
По минимальному D 2 выбираем гипотезу Н 2 – неисправность датчика температуры 2. После того как поработала бригада ремонтников, возможны 2 исхода:
1. Гипотеза Н 2 подтвердилась.
2. Гипотеза Н 2 не подтвердилась.
Рассмотрим первый вариант. Пусть N 2 = 10. Гипотеза Н 2 подтвердилась, следовательно, корректируем значения  ,
,  и
и 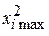 .
.
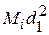 = (
= (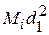 × 10 + x 1) / (10 + 1) = (5 × 10 + 4) / 11 = 4,93 %;
× 10 + x 1) / (10 + 1) = (5 × 10 + 4) / 11 = 4,93 %;
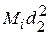 = (0,5 × 10 + 0,2) / 11 = 0,49 %;
= (0,5 × 10 + 0,2) / 11 = 0,49 %;
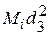 = (3 × 10 + 4) / 11 = 3,09 %;
= (3 × 10 + 4) / 11 = 3,09 %;
 = (0 × 10 + 0,1) / 11 = 0,009 %;
= (0 × 10 + 0,1) / 11 = 0,009 %;
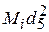 = (4 × 10 + 2) / 11 = 3,86 %;
= (4 × 10 + 2) / 11 = 3,86 %;
 и
и 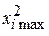 остаются прежними, так как xi попадает в существующий промежуток, кроме x 5;
остаются прежними, так как xi попадает в существующий промежуток, кроме x 5;
 = 2 %; N 2 = N 2 + 1 = 11.
= 2 %; N 2 = N 2 + 1 = 11.
Рассмотрим второй вариант. Гипотеза Н 2 не подтвердилась. В реальности отказал водосчетчик 1, т.е. имела место гипотеза Н 1. Пусть N 1 = 10, как и в предыдущем случае.
Корректируем значения  ,
, 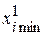 и
и  .
.
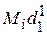 = (5 × 10 + 4) / 11 = 4,93 %;
= (5 × 10 + 4) / 11 = 4,93 %;
 = (0,5 ×10 + 0,2) / 11 = 0,49 %;
= (0,5 ×10 + 0,2) / 11 = 0,49 %;
 = (3 × 10 + 4) / 11 = 3,09 %;
= (3 × 10 + 4) / 11 = 3,09 %;
 = (0 × 10 + 0,1) / 11 = 0,009 %;
= (0 × 10 + 0,1) / 11 = 0,009 %;
 = (0,6 ×10 + 2) / 11 = 0,73 %;
= (0,6 ×10 + 2) / 11 = 0,73 %;
 = 2 %; N 1 = N 1 + 1 = 11.
= 2 %; N 1 = N 1 + 1 = 11.
Получим нечеткое множество неисправностей для текущего шага работы экспертной системы, где коэффициенты принадлежности, как и в предыдущем случае, определяют вероятность появления данной гипотезы.
На данном шаге были получены следующие значения:
Н 1 = 2,225; Н 2 = 1,425; Н 3 = 10,46; Н 4 = 9,56.
Далее делим значения для гипотез на сумму значений гипотез по формуле
 . (4.21)
. (4.21)
Н 1 = 0,09; Н 2 = 0,057; Н 3 = 0,426; Н 4 = 0,389.
После этого преобразуем полученные значения по формуле
 . (4.22)
. (4.22)
Получим следующие вероятности: p 1 = 0,3; p 2 = 0,31; p 3 = 0,189; p 4 = 0,201.
Тогда нечеткое множество для диагностики системы будет выглядеть следующим образом:
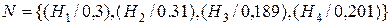 ,
,
т.е. гипотеза Н 1 имеет место с вероятностью 0,3, гипотеза Н 2 – с вероятностью 0,31, гипотеза Н 3 – с вероятностью 0,189 и гипотеза Н 4 – с вероятностью 0,201.
Теперь рассмотрим на примере, как определить, достаточно ли данного количества шагов для того, чтобы считать экспертную систему обученной.
Пусть для нашей экспертной системы заданная вероятность правильного ответа – 0,7 с 85%-м доверительным интервалом. Предположим, что было произведено 200 шагов обучения экспертной системы. На последних шагах новые примеры перестали сказываться на точности классификации. Следовательно, процесс обучения закончен. Подсчитаем, какова вероятность правильного ответа экспертной системы. Экспертная система дала правильный ответ в 68 случаях из 200. Тогда p * = 0,34. Определим 85%-й доверительный интервал. Просчитаем по формулам (4.13) и (4.14) (так как n больше 100) p 1 и p 2:
p 1 = 0,292; p 2 = 0,388; I b = (0,292, 0,388).
Таким образом, с вероятностью 0,85 вероятность правильного ответа экспертной системы будет находиться в границах от 0,292 до 0,388. Полученная вероятность правильного ответа нас не удовлетворяет, следовательно, нужно вернуться на этап выбора параметров, проанализировать полученную таблицу функций неисправностей и добавить недостающие параметры, после чего заново провести обучение системы. Этот процесс придется повторять до тех пор, пока нижняя граница вероятности правильного ответа экспертной системы p 1 не станет выше заданной.






