В данном разделе представлен метод контроля программ по ГСА, где двоичное представление команд интерпретируется как двоичное представление коэффициентов полинома соответствующей степени.
Суть метода заключается в следующем. В ГСА выделяются линейные фрагменты, заключенные между двумя условными операторами.
Пример 4.15. На рис. 4.48 представлена ГСА; 7 линейных фрагментов, на которые она разбивается, приведены на рис. 4.49.
Каждому линейному фрагменту ставится в соответствие полином Мh (х):
где h – порядковый номер фрагмента; k – количество операторных вершин в линейном фрагменте; f – количество разрядов в двоичной комбинации каждой операторной вершины.
Рис. 4.48. Пример ГСА
|
Пример 4.16. В табл. 4.2 (см. ниже) приведена двоичная запись каждой операторной вершины ГСА (см. рис. 4.48). Рассмотрим линейный фрагмент, показанный на рис. 4.49, в данной ГСА f = 4, для данного линейного фрагмента k = 2, так как во фрагмент входят две операторные вершины А5 и А6, которым соответствуют двоичные комбинации { a 4 a 1}. Полином будет выглядеть следующим образом:
В окончательном виде для данного фрагмента
.
Совокупность полиномов Mh (x) разбивается на два подмножества. К первому подмножеству относятся полиномы, описывающие последовательности, расположенные после начальной вершины Ан или единичного выхода условных вершин, а ко второму подмножеству – полиномы, описывающие последовательности, расположенные после нулевого выхода условных вершин.
Рис. 4.49. Линейные фрагменты ГСА
Далее выбирается G (x) – проверяющий полином. Для упрощения преобразований рекомендуется выбирать проверяющий полином вида G (х) = хq + 1, где q кратно разрядности кода операторных вершин.
Для каждого подмножества выбирается R эт(х) – эталонный остаток от деления Мh (х) на G (х). Если для какого-то полинома его остаток Rh (x) не совпадает с эталоном своего подмножества, то Mh (x) корректируется.
Полином Mh (x) приводится к эталонному остатку в два этапа.
Таблица 4.2
| Разбиение ГСА на подмножества | Подмножество 1 | Подмножество Æ |
| a 1: 1011 a 4: 0101 a 2: 1101 a 5: 0010 a 3: 0110 a 6: 1010 | 1. A1 – A2 2. A3 – A4 3. A5 – A6 4. A8 – A7 – A2 | 1. A9 2. A5 – A6 3. Æ |
| Rh (x) | k (x) | ||
| П1 | 1. А1 – А2(а 1, а 2) 2. А3 – А4(а 3, а 2) 3. А8 – А7 – А2(а 3, а 5, а 2) 4. Æ | 1101 А1д 1111 А3д 0110А4д | |
| П2 | 1. А9(а 6) 2. А5 – А6(аn, а 1) | 0100А2д |
Первоначально выполняется преобразование
,
где M ¢ h (x) – полином, соответствующий последовательности, в которую введена пустая дополнительная вершина; M 1 h (x) – полином степени (fz 1–1), описывающий z 1 операторных вершин, расположенных до введения пустой последовательности; M 2 h (x) – полином cтепени (ft 2–1), описывающий z 2 операторных вершин, расположенных после введенной пустой вершины.
Затем
,
где M " h (x) – преобразовательный полином; k (х) – корректирующий полином степени q –1; t – коэффициент, определяющий расположение k (х) относительно фрагмента M ¢ h (x), соответствующего пустой вершине.
При этом
.
Пример 4.17. Выполним разбиение ГСА, приведенной на рис. 4.48. Коды, соответствующие каждой операторной вершине, и разбиение на подмножества 1 и 0 приведены в табл. 4.2. Третий элемент подмножества 0, представляющий собой пустое множество, соответствует переходу по нулю из P1 в P2. Элемент 3 подмножества 1 и элемент 2 подмножества 0 совпадают – {A5, A6}. Поэтому условие P1 инвертируется на 
и соответственно выход по 1 (0) меняется на выход по 0 (1). Таким образом, в подмножестве 1 будут элементы {A1,A2}, {A3,A4}, {A8,A6,A2}, {0}, а в подмножестве 0 – {A9}, {A5, A6}.
В качестве проверяющего выберем полином G (x) = x 4 + 1.
В табл. 4.2 приведены Rh (x) для каждого подмножества. Для подмножества 1 в качестве эталонного остатка выбран R 1эт(х) = 0110, а для подмножества 0 R 0эт(х) = 1010. Соответственно для каждого элемента указаны корректирующий полином k (x) и его обозначение.
На рис. 4.50 приведена преобразованная ГСА с введенными диагностическими вершинами.
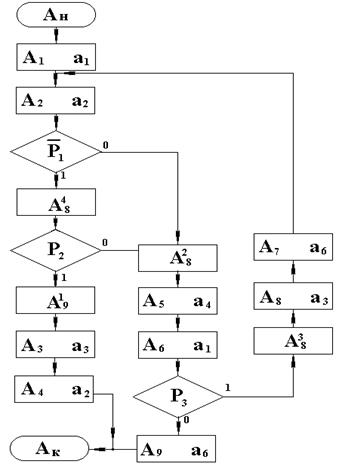Рис. 4.50.Преобразованная ГСА
|
СВК для данного метода показана на рис. 4.51. На СВК возлагается выполнение следующих функций:
– формирование фактических остатков;
– хранение и выборка эталонных остатков;
– сравнение фактических и эталонных остатков;
– формирование сигнала диагностирования.
Рис. 4.51.СВК на основе полиноминальной интерпретации
СС – схема свертки, представляющая собой параллельный регистр сдвига с обратными связями, СХЭ – схема хранения эталонного остатка, выборка из которой определяется значением набора логических условий, соответствующего контролируемой последовательности. УУ формирует два дополнительных сигнала:
– признак диагностической вершины;
– признак конца последовательности.
Вероятность обнаружения дефектов по этому методу главным образом зависит от степени проверяющего полинома, как для дефектов механизма хранения, так и для дефектов механизма дешифрации команд:
Р обн = 1 – 0,5 q.
K изб для данного метода равно 0, так как избыточных разрядов в команду не вводится.
Избыточное время зависит от количества линейных фрагментов, и в худшем случае
где Н 0 – количество линейных фрагментов в нулевом подмножестве; Н 1 – количество линейных фрагментов в единичном подмножестве; N – общее число команд.
Задержка обнаружения дефекта аналогична задержке по методу сигнатур. СВК реализуется несколько проще, чем для контроля сигнатур, но сложнее, чем для контроля с помощью раскраски, и не является самопроверяемой.
