Алгоритмы обучения экспертных систем

 

Изложим теперь алгоритмы обучения экспертной системы в общем виде. Алгоритм обучения для системы, принимающей решения по макси­мальной вероятности, выглядит следующим образом:

1. Провести наблюдения на объекте, который должен быть класси­фицирован и получить .

2. Вычислить значение (4.7):

для каждой категории. На первом шаге все b_i для всех категорий и, следо­вательно, все y равны 0, однако следует сохранить этот этап и на первом шаге для единообразия алгоритма.

3. Найти такую категорию k, для которой y_k имеет наибольшее зна­чение.

4. Если такая категория есть и объект действительно к ней принад­лежит, то такая классификация корректна. Перейти к п. 6.

5. Если указанная попытка не удалась, то проводим следующую мо­дификацию: b_ik = b_ik + x_i для той категории k, куда, согласно классифика­ции, должен был попасть объект; b_ir = b_ir + x_i для всех категорий r, в кото­рые данный объект не должен был попасть, но для которых y_r ³ y_k.

6. Провести очередное наблюдение на объекте и перейти к п. 2.

Система считается обученной, если процент правильных классифи­каций удовлетворяет пользователя либо если новые примеры для обучения перестают влиять на точность классификации.

Алгоритм обучения правил системы, принимающей решения по наименьшему расстоянию, будет следующим:

1. Провести наблюдения на объекте, который должен быть класси­фицирован, и получить .

2. Вычислить значение

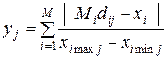(4.8)

для каждой категории, где M_id_ij – среднее значение для j гипотезы, а х_{i max j} и х_{i min j} – соответственно максимальное и минимальное значение. На пер­вом шаге все средние, максимальные и минимальные значения для всех категорий равны 0 (если не принимают какие-то отличные от 0 значения в соответствии с опытом разработчика) и, следовательно, все y_j равны 0, од­нако этот этап сохраняется и на первом шаге для единообразия алгоритма.

3. Найти такую категорию (гипотезу) k, для которой y_k имеет наи­меньшее значение.

4. Если такая категория есть и объект действительно к ней принад­лежит, то такая классификация проведена успешно. Корректировка прово­дится одинаково как в случае успешной, так и в случае неуспешной клас­сификации. Н_k – категория, которая имела место на объекте в данном ис­пытании. Пусть N_k – число корректировок категории Н_k (начальное значе­ние N_k равно 1). Тогда

. (4.9)

 

5. Провести очередное наблюдение на объекте и перейти к п. 2.

Система считается обученной, если процент правильных классифи­каций удовлетворяет пользователя либо если новые примеры для обучения перестают влиять на точность классификации.

Рассмотрим подробнее методику обучения экспертной системы. Для периода обучения можно выделить несколько этапов. На первом этапе оп­ределяется набор гипотез технического состояния системы и параметров, основываясь на которых система будет выносить заключение о вероятно­сти той или иной гипотезы. Набору гипотез и параметров следует уделить особое внимание, поскольку в процессе обучения ни то ни другое нельзя изменять. В общем случае будем руководствоваться следующими сообра­жениями. Поскольку мы создаем экспертную систему для диагностики, то в качестве предельного случая следует задать набор гипотез, совпадающих с полным набором всех возможных как однократных, так и кратных неис­правностей. Как правило, такой полный перечень гипотез на практике не­осуществим, поэтому в качестве оптимального варианта примем набор ги­потез, совпадающий с полным набором всех возможных однократных не­исправностей блоков системы.

При выборе списка параметров, по которым экспертная система бу­дет выносить решение о наличии той или иной неисправности, следует учесть, что для сложной технической системы, особенно при наличии в ней аналоговых узлов, очень трудно заранее предсказать, какие именно па­раметры дадут экспертной системе возможность составить правильное за­ключение. Поэтому в список параметров следует вводить возможно боль­шее их количество, при этом желательно в качестве параметров эксперт­ной системы принимать не только значения физических характеристик ди­агностируемой системы, но и соотношения между ними. Процесс выбора параметров экспертной системы неформализуем, однако именно от него в первую очередь зависит успешный исход всего проекта.

После того как закончен этап выбора гипотез и параметров, следует этап обучения экспертной системы. На этапе обучения система устанавли­вает для себя правила, которыми она будет руководствоваться в рабочем режиме. Понятно, что при большом количестве гипотез количество на­блюдений, которые необходимы системе для выведения правил, неограни­ченно растет. Для ускорения процесса обучения можно воспользоваться двумя способами.

Первый способ заключается в построении модели, математической или физической, что позволит вводить неисправности не в естественном темпе их появления в системе, а непосредственно одну за другой. Если мо­дель построить не удается, но диагностируемая система позволяет вре­менно выводить себя из рабочего режима и вносить требуемые неисправ­ности, то время обучения также может быть сокращено.

Алгоритм обучения утверждает, что система считается обученной, если процент правильных классификаций удовлетворяет пользователя либо если новые примеры для обучения перестают влиять на точность классификации. Очевидно, что второй вариант является менее желатель­ным, но в этом случае следует определить, какая же вероятность правиль­ного ответа была достигнута.

Для определения момента конца обучения воспользуемся аппаратом математической статистики.

Пусть событие А – это правильный ответ экспертной системы. Будем оценивать вероятность p события А по его частоте p ^* в n независимых опы­тах. Величина Х будет принимать значение 1, если событие появилось (экспертная система дала правильный ответ), и 0 в противном случае.

Частота события находится по следующей формуле:

. (4.10)

В качестве точечной оценки для неизвестной вероятности p разумно принимать частоту p ^*.При этом возникает вопрос о построении довери­тельного интервала для вероятности p.

Для вероятности p доверительный интервал I _b = (p ₁, p ₂), где b – вероят­ность того, что истинная вероятность попадет в указанный интервал.

Выбор формулы для подсчета доверительного интервала зависит от n. Если число опытов не превосходит 100, то p ₁ и p ₂ находятся по следую­щим формулам:

; (4.11)

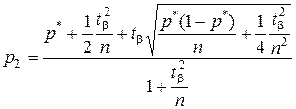, (4.12)

где t _b – коэффициент Стьюдента, взятый из таблицы для заданного b.

Для больших n (порядка сотен) можно пользоваться следующими фор­мулами:

, (4.13)

. (4.14)

Приведем значения коэффициентов Стьюдента в зависимости от за­данной вероятности (табл. 4.3).

Таблица 4.3

 

b	t b	b	t b	b	t b	b	t b
0,80	1,282	0,86	1,475	0,91	1,694	0,97	2,169
0,81	1,310	0,87	1,513	0,92	1,750	0,98	2,325
0,82	1,340	0,88	1,554	0,93	1,810	0,99	2,576
0,83	1,371	0,89	1,597	0,94	1,880	0,9973	3,000
0,84	1,404	0,90	1,643	0,95	1,960	0,999	3,290
0,85	1,439			0,96	2,053

Из всего вышеприведенного следует общий алгоритм обучения экс­пертной системы:

1. В качестве исходных данных к проекту задаемся вероятностью правильного ответа экспертной системы и доверительной вероятностью.

2. Определяем набор гипотез и параметров экспертной системы. Если это возможно, строим модель диагностируемой системы.

3. Проводим очередное испытание экспертной системы: предъявляем текущий набор параметров и получаем выбранную экспертной системой гипотезу.

4. В соответствии с методом обучения экспертная система проводит модификацию правил.

5. Увеличивая количество испытаний n на единицу, с учетом общей частоты правильных ответов находим p ₁ и p ₂. Если p ₁ выше заданной веро­ятности правильного ответа, считаем, что процесс обучения закончен, если нет, переходим к п. 3. Однако возможно возникновение такой ситуации, когда новые примеры перестали влиять на точность классификации. Это значит, что принятый на этапе 2 набор параметров не является удачным. Следует его расширить, а возможно, и ввести в систему новые датчики, т.е. вернуться к п. 2.

Для улучшения набора параметров логично воспользоваться инфор­мацией, накопленной экспертной системой в процессе обучения. Фактиче­ски экспертная система формирует таблицу функций неисправностей (табл. 4.4).

Таблица 4.4

 

Параметр	Н 1	Н 2	…	НN
	р 11	р 12		р 1 N
	р 21	р 22		р 2 N
…
М	рМ 1	рМ 2		рМN

 

В этой таблице р_ij обозначает значение параметра i при наличии ги­потезы Н_j. Анализ этой таблицы позволит выявить гипотезы, которые экс­пертная система не в состоянии различить. Для таких гипотез значения столбцов таблицы функций неисправностей будут совпадать. Следова­тельно, разумно дополнить экспертную систему новыми параметрами, ко­торые помогут снять это совпадение.

Предположим, что процесс обучения экспертной системы завершился успешно и вероятность правильного ответа превышает заданную. Однако мы уже видели, что вероятность правильного ответа все равно никогда не достигнет единицы. Следовательно, в большинстве случаев будет разумно выдавать не одну подозреваемую неисправность, для которой вероятность возникновения наиболее велика, а несколько подозреваемых неисправно­стей с наибольшими вероятностями.

Таким образом, мы приходим к нечеткому множеству неисправно­стей N, характеристическая функция m _А (х) для которых будет представлять собой вероятность того, что на данный момент времени в системе имеется именно данная неисправность, т.е. в нечеткое множество будут входить принятые гипотезы со своими коэффициентами принадлежности к множе­ству всех возможных гипотез:

 

.

 

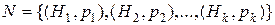В соответствии с математическим аппаратом значения р_i должны на­ходиться на интервале (0;1). Покажем, как преобразовать значения гипотез в вероятности для обоих методов построения правил экспертной системой:

1. Для экспертной системы, ориентированной на максимальную ве­роятность, имеем набор значений y_{k .} В случае если среди полученных зна­чений имеются отрицательные, складываем полученные значения с y_{k min}. Затем делим эти коэффициенты на их общую сумму.

2. Для экспертной системы, принимающей решения на основании выбора по наименьшему расстоянию, методика определения коэффициен­тов характеристической функции будет иная, поскольку, чем меньше под­считанное значение гипотезы, тем более она вероятна. В соответствии с алгоритмом здесь отрицательные значения y_k не могут быть получены.

Далее делим значения для гипотез на сумму значений гипотез:

 

. (4.15)

 

После этого преобразуем полученные значения по формуле

 

. (4.16)

 

Таким образом, нечеткое множество подозреваемых неисправностей может быть сформировано для обоих вариантов построения экспертной системы.

Поскольку имеется два способа построения решающих правил для экспертной системы, невозможно заранее предсказать, какой из них окажется лучшим. Однако если есть возможность довольно точно заранее оценить средние значения параметров, то можно ожидать, что система, обучаемая по средним значениям, станет работоспособной быстрее.

В общем случае целесообразно построить оба варианта системы, а после обучения выбрать ту, которая лучше себя ведет.

Рассмотрим оба принципа обучения на конкретном примере экс­пертной системы технического диагностирования (ЭСТД) такого сложного объекта, как АСУ ТП «интеллектуального здания», в состав которой вхо­дят персональные компьютеры, интеллектуальные датчики, исполнитель­ные устройства автоматики, регуляторы и т.д. Подобная ЭСТД сможет принимать решения об исправности или неисправности тех или иных уз­лов АСУ ТП.

4.4.5. АСУ «интеллектуальным зданием»

Современное офисное здание должно способствовать продуктивной деятельности организации за счет эффективного управления целым ком­плексом подсистем информационного и инженерного обеспечения.

В основу идеологии «интеллектуального здания» заложено макси­мальное использование возможностей современных средств информаци­онных технологий с целью повышения экономичности, безопасности, а также надежностных, эксплуатационных и экономических показателей жизнедеятельности здания.

К информационному и техническому обеспечению современного административно-производственного здания, предназначенного для обес­печения деятельности предприятия со сложным производственным про­цессом, предъявляются повышенные требования.

Система автоматизации управления (интеллектуализации) зданием может быть отнесена к классу интегрированных диспетчерских систем. На пульт диспетчера (оператора здания) поступает в необходимой форме ин­формация о состоянии различного оборудования и подсистем здания. На основании анализа информации оператор выполняет необходимые дейст­вия, сведения о направленности и содержании которых он получает с эк­рана пульта. Наряду с этим оператору могут быть предоставлены широкие возможности для контроля за выделенным множеством параметров жизне­обеспечения здания, а также необходимые функции управления.

Помимо функций контроля и управления система должна обеспечи­вать формирование в необходимой форме отчетов, статистик, а также ин­тегрированных показателей жизнедеятельности здания (энергопотребление и т.д.).

Топологическая структура системы представлена на рис. 4.52. Она включает в себя ряд подсистем, а также источники информации о состоя­нии отдельных элементов здания.

Рис. 4.52. Топологическая структура АСУ ТП «интеллектуального здания»

 

В качестве примера для демонстрации методики построения само­обучаемой экспертной системы возьмем подсистему горячего водоснабже­ния этажа, связанную по кольцу сетью с центром управления здания (рис. 4.53).

 

Рис. 4.53. Структурная схема подсистемы горячего водоснабжения этажа

 

Для каждого помещения этажа на трубопроводе установлены пока­зывающие датчики давления, температуры и водосчетчик.

Кроме того, общими для всех этажей являются два водоподогрева­теля I и II ступеней, пять насосов, регулятор температуры (РТ) и связанный с ним датчик температуры (ДТ). Неизрасходованная потребителем горячая вода поступает на вход водоподогревателя второй ступени.

Подсистема контролирует температуру горячей воды на выходе во­доподогревателя второй ступени и давление горячей воды в циркуляцион­ном трубопроводе.

Управление происходит следующим образом. Если температура ниже нормы, то необходимо увеличить расход сетевой воды во второй ступени, если выше нормы, то уменьшить расход. Если при проделанных операциях температура горячей воды не станет нормальной, то подается сигнал аварии.

Применительно к АСУ ТП x_i – это совокупность параметров сис­темы, полученных при замере этих параметров в какой-либо конкретный момент времени, b_i – это заложенные в экспертную систему на основании опыта или гипотетических заключений коэффициенты для вычисления окончательного решения.

Отсюда видно, что основная сложность при разработке экспертной системы – определение коэффициентов b_i. Достаточно часто невозможно предварительно с помощью математических методов промоделировать ра­боту системы и определить, какими будут параметры при отказе исследуе­мого узла. В этом случае существует возможность построения обучаемой экспертной системы, когда система по известным x_i и y сама определяет b_i.

 

4.4.6. Система, принимающая решения по максимальной вероятности

 

Для большей наглядности обучающий алгоритм будем иллюстриро­вать на выделенных узлах подсистемы горячего водоснабжения АСУ ТП, структурная схема которых приведена на рис. 4.54.

 

Рис. 4.54. Структурная схема узла подсистемы горячего водоснабжения

 

Горячая вода поступает в два помещения, при этом на трубопрово­дах установлены для первого помещения водосчетчик 1, датчик темпера­туры 2 и датчик давления 5, для второго помещения водосчетчик 3, датчик температуры 4 и датчик давления 6. Показания всех счетчиков выведены на пульт оператора. В системе здания присутствуют общие водонагрева­тели, насосы, а также регулятор температуры и связанный с ним датчик температуры. Поскольку температура и расход воды непосредственно свя­заны алгоритмом управления, контролировать показания водосчетчиков и датчиков температуры на этаже можно по показаниям общего датчика температуры и расхода воды.

Предположим, что может произойти отказ одного любого из датчи­ков 1, 2, 3 и 4 (чтобы не усложнять пример). Тогда при выявлении непола­док в системе горячего водоснабжения следует выбрать одну из четырех гипотез:

Н ₁ – неисправен водосчетчик 1;

Н ₂ – неисправен датчик температуры 2;

Н ₃ – неисправен водосчетчик 3;

Н ₄ – неисправен датчик температуры 4.

Опираться мы будем на следующую систему наблюдений:

Х ₁ – совпало ли показание датчика температуры 2 с показаниями об­щего датчика температуры, откорректированного по расходу воды?

Х ₂ – совпало ли показание датчика температуры 4 с показаниями об­щего датчика температуры, откорректированного по расходу воды?

Х ₃ – совпало ли показание водосчетчика 1 с показаниями общего датчика температуры, откорректированного по расходу воды?

Х ₄ – совпало ли показание водосчетчика 2 с показаниями общего датчика температуры, откорректированного по расходу воды?

Х ₅ – соответствуют ли показания водосчетчиков общему расходу воды в системе?

Значением наблюдения будет 1, если ответ на соответствующий во­прос утвердительный, и 0, если ответ отрицательный.

Эти 5 чисел (М = 5) и будут выступать как х_i в формуле (4.7). Отно­сительно коэффициентов b_i сложно что-либо сказать на начальном этапе обучения, поэтому их принимают равными нулю.

Напомним алгоритм выработки правил (рис. 4.55).

Проиллюстрируем данный алгоритм обучения на примере.

Пусть неисправен водосчетчик 1 (однако нам пока неизвестно, что имела место именно эта неисправность). Тогда (предположительно, а в процессе обучения реальной системы значения замеров будут известны точно)

 

Х ₁ = 0; Х ₂ = 1; Х ₃ = 0; Х ₄ = 1; Х ₅ = 1.

 

Вычисляем y для каждой гипотезы:

Н ₁: y ₁ = b ₁₁ x ₁ + b ₂₁ x ₂ + b ₃₁ x ₃ + b ₄₁ x ₄ + b ₅₁ x ₅ = 0;

Н ₂: y ₂ = b ₁₂ x ₁ + b ₂₂ x ₂ + b ₃₂ x ₃ + b ₄₂ x ₄ + b ₅₂ x ₅ = 0;

Н ₃: y ₃ = b ₁₃ x ₁ + b ₂₃ x ₂ + b ₃₃ x ₃ + b ₄₃ x ₄ + b ₅₃ x ₅ = 0;

Н ₄: y ₄ = b ₁₄ x ₁+ b ₂₄ x ₂ + b ₃₄ x ₃ + b ₄₄ x ₄+ b ₅₄ x ₅ = 0.

 

Рис. 4.55. Алгоритм выработки правил для системы, принимающей решения по макси­мальной вероятности

 

Так как все y одинаковы, неисправность проклассифицировать нельзя. Поэтому ремонтной бригадой проводятся работы по обнаружению причины неисправности (и естественно, ее устранению). После этого мы узнаем, какая из гипотез оказалась правильной, и можем передать это зна­ние экспертной системе. В соответствии с алгоритмом для той категории, в которую должен был попасть объект (категория Н ₁), проводится модифи­кация коэффициентов b:

 

b ₁₁ = b ₁₁ + x ₁ = 0; b ₂₁ = b ₂₁ + x ₂ = 1;

b ₃₁ = b ₃₁ + x ₃ = 0; b ₄₁ = b ₄₁ + x ₄ = 1;

b ₅₁ = b ₅₁ + x ₅ = 1.

 

Для тех категорий, в которые объект не должен был попасть, но у ко­торых y_k больше, чем y правильной категории или равен ему (в данном случае, это категории Н ₂, Н ₃ и Н ₄), проводится другая модификация коэф­фициентов b.

Для категории Н ₂: b ₁₂ = b ₁₂ – x ₁ = 0; b ₂₂ = b ₂₂ – x ₂ = –1; b ₃₂ = b ₃₂ – x ₃ = 0; b ₄₂ = b ₄₂ – x ₄ = –1; b ₅₂ = b ₅₂ – x ₅ = –1.

Для категории Н ₃: b ₁₃ = b ₁₃ – x ₁ = 0; b ₂₃ = b ₂₃ – x ₂ = –1; b ₃₃ = b ₃₃ – x ₃ = 0; b ₄₃ = b ₄₃ – x ₄ = –1; b ₅₃ = b ₅₃ – x ₅ = –1.

Для категории Н ₄: b ₁₄ = b ₁₄ – x ₁ = 0; b ₂₄ = b ₂₄ – x ₂ = –1; b ₃₄ = b ₃₄ – x ₃ = 0; b ₄₄ = b ₄₄ – x ₄ = –1; b ₅₄ = b ₅₄ – x ₅ = –1.

Первый шаг закончен.

Возникла очередная неисправность – начался второй шаг обучения.

Снова вычисляем y для каждой гипотезы с новыми коэффициентами. Пусть на этот раз неисправен датчик температуры 2. Тогда результаты на­блюдений будут (предположительно) следующими:

 

Х ₁ = 0; Х ₂ = 1; Х ₃ = 0; Х ₄ = 1; Х ₅ = 0.

 

Для Н ₁ y ₁ = 0 × 0 + 1 × 1 + 0 × 0 + 1 × 1 + 1 × 0 = 2;

Для Н ₂ y ₂ = 0 × 0 + (–1) × 1 + 0 × 0 + (–1) × 1 + (–1) × 0 = –2;

Для Н ₃ y ₃ = 0 × 0 + (–1) × 1 + 0 × 0 + (–1) × 1 + (–1) × 0 = –2;

Для Н ₄ y ₄ = 0 × 0 + (–1) × 1 + 0 × 0 + (–1) × 1 + (–1) × 0 = –2.

 

Получено максимальное значение y для гипотезы Н ₁, а должно быть – для гипотезы Н ₂. Объект снова не попал в нужную категорию, и модифи­кацию коэффициентов приходится повторить.

Для категории Н ₂: b ₁₂ = b ₁₂ + x ₁ = 0 + 0 = 0; b ₂₂ = b ₂₂ + x ₂ = (–1) + 1 = 0; b ₃₂ = b ₃₂ + x ₃ = 0 + 0 = 0; b ₄₂ = b ₄₂ + x ₄ = (–1) + 1 = 0; b ₅₂ = b ₅₂ + x ₅ = (–1) + 0 = = –1.

Для категории Н ₁: b ₁₁ = b ₁₁– x ₁ = 0 – 0 = 0; b ₂₁ = b ₂₁ – x ₂ = 1 – 1 = 0; b ₃₁ = = b ₃₁ – x ₃ = 0 – 0 = 0; b ₄₁ = b ₄₁ – x ₄ = 1 – 1 = 0; b ₅₁ = b ₅₁ – x ₅ = 1 – 0 = 1.

Для категории Н ₃: b ₁₃ = b ₁₃ – x ₁ = 0 – 0 = 0; b ₂₃ = b ₂₃ – x ₂ = (–1) –1 = –2; b ₃₃ = b ₃₃ – x ₃ = 0 – 0 = 0; b ₄₃ = b ₄₃ – x ₄ = (–1) – 1 = –2; b ₅₃ = b ₅₃ – x ₅ = (–1) – 0 = = –1.

Для категории Н ₄: b ₁₄ = b ₁₄ – x ₁ = 0 – 0 = 0; b ₂₄ = b ₂₄ – x ₂ = (–1) –1 = –2; b ₃₄ = b ₃₄ – x ₃ = 0 – 0 = 0; b ₄₄ = b ₄₄ – x ₄ = (–1) – 1 = –2; b ₅₄ = b ₅₄ – x ₅ = (–1) – 0 = = –1;

Второй шаг окончен.

Теперь сделаем третий шаг. Очередная неисправность снова оказа­лась неисправностью водосчетчика 1. В этом случае, как уже упоминалось,

 

Х ₁ = 0; Х ₂ = 1; Х ₃ = 0; Х ₄ = 1; Х ₅ = 1.

 

Подсчитаем значения y для всех гипотез, используя последние мо­дификации коэффициентов b.

 

Для Н ₁: y ₁ = 0 × 0 + 0 × 1 + 0 × 0 + 0 × 1 + 1 × 1 = 1;

Для Н ₂: y ₂ = 0 × 0 + 0 × 1 + 0 × 0 + 0 × 1 + (–1) × 1 = –1;

Для Н ₃: y ₃ = 0 × 0 + (–2) × 1 + 0 × 0 + (–2) × 1 + (–1) × 1 = –5;

Для Н ₄: y ₄ = 0 × 0 + (–2) × 1 + 0 × 0 + (–2) × 1 + (–1) × 1 = –5.

 

Наибольшее значение y ₁ указывает на гипотезу Н ₁, что является пра­вильным результатом. Поэтому модификация коэффициентов не прово­дится.

Пусть для нашей экспертной системы заданная вероятность пра­вильного ответа – 0,7 с 90%-м доверительным интервалом. Предположим, что мы провели 100 шагов обучения. Подсчитаем, с какой вероятностью мы можем доверять решениям экспертной системы. Пусть экспертная сис­тема дала правильный ответ в 78 случаях из 100. Тогда p ^* = 0,78. Опреде­лим 90%-й доверительный интервал для вероятности правильного ответа экспертной системы. Просчитаем по формулам (4.11), (4.12) (поскольку n = = 100) p ₁ и p ₂:

 

p ₁ = 0,705; p ₂ = 0,840; I _b = (0,705; 0,840).

 

Таким образом, с вероятностью 0,9 вероятность правильного ответа экспертной системы будет находиться в границах от 0,705 до 0,840. Пусть для нашей экспертной системы заданная вероятность правильного ответа – 0,7. Следовательно, на данном шаге обучение может быть закончено.

Получим нечеткое множество неисправностей для текущего шага ра­боты экспертной системы, где коэффициенты принадлежности определяют вероятность появления данной гипотезы. Фактически, нам надо для каж­дой гипотезы определить ее коэффициент принадлежности:

1. На данном шаге были получены следующие значения: Н ₁ = 1; Н ₂ = = –1; Н ₃ = –5; Н ₄ = –5.

2. Складываем полученные значения с Н _min. Получаем следующие коэффициенты: Н ₁ = 6; Н ₂ = 4; Н ₃ = 0; Н ₄ = 0.

3. Затем делим эти коэффициенты на их общую сумму. В данном случае .

Следовательно, получим вероятности появления каждой гипотезы на текущем шаге, т.е. коэффициенты принадлежности каждой гипотезы к множеству возможных неисправностей АСУ ТП:

 

p ₁ = 0,6; p ₂ = 0,4; p ₃ = 0; p ₄ = 0.

 

Тогда нечеткое множество гипотез о возможных неисправностях АСУ ТП для диагностики системы будет выглядеть следующим образом:

 

N = {(Н ₁/0,6), (Н ₂/0,4), (Н ₃/0), (Н ₄/0)},

 

т.е. гипотеза Н ₁ имеет место с вероятностью 0,6; гипотеза Н ₂ – с вероятно­стью 0,4; гипотеза Н ₃ – с вероятностью 0; гипотеза Н ₄ также с вероятно­стью 0.