Приборы, построенные по компенсационной схеме (схеме с обратной связью), имеют малую как аддитивную, так и мультипликативную погрешности. Применение обратной связи позволяет создать приборы, обладающие малой статической и динамической погрешностью. Эти приборы имеют большую выходную мощность, и их показания мало зависят от нагрузки.
Структурная схема компенсационного преобразователя приведена на рис. 4.5. Входная величина х подается на один из входов вычитающего преобразователя, на другой его вход подается сигнал х ос, той же физической природы, что и входная величина х, причем размер величины х ос определяется размером выходной величины у Разность D x = х – хос,поступает в преобразователь 1. Если преобразователи 1, 2 имеют линейные функции преобразования
(4.36)
где S1 и S2 – чувствительности соответствующих преобразователей, то зависимость между входной величиной х и сигналом х ос определяется соотношением
(4.37)
Из (4.37) следует
(4.38)
Произведение S1S2 часто достаточно велико, и можно считать, что х» хос. Равенство х» хос часто имеет место и при нелинейных функциях преобразования преобразователей. С другой стороны, х осявляется функцией выходной величины
(4.39)
Из этого соотношения можно определить
(4.40)
где f -1 – обозначение функции, обратной (4.39).
Следовательно, если х» хос то у определяется преобразователем 2 (рис. 4.5) и мало зависит от преобразователя 1. В приборах с обратной связью роль преобразователя обратной связи выполняют простые устройства, обладающие высокой точностью. При этом высокую точность имеет и прибор в целом.
Рассмотрим функцию преобразования и чувствительность преобразователя с обратной связью. Для простоты положим, что преобразователи 1 и 2 на схеме рис. 4.5 имеют пропорциональные функции преобразования (4.36).
Имея в виду равенства (4.36) и
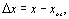(4.41)
получаем
(4.42)
Отсюда чувствительность схемы с обратной связью
(4.43)
Определим погрешность устройства, обусловленную мультипликативными погрешностями входящих в него преобразователей 1 и 2, т.е. погрешность, вызванную непостоянством чувствительностей этих преобразователей.
Согласно (4.43) чувствительность схемы является функцией двух переменных
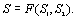(4.44)
Изменение S можно определить как полный дифференциал выражения (4.44):
(4.45)
Входящие в (4.45) частные производные получаются путем дифференцирования (4.43):
(4.46)
(4.47)
Подставив (4.46) и (4.47) в (4.45), получим
(4.48)
Относительная мультипликативная погрешность d y = D y/y равна относительному изменению чувствительности D S/S. Учитывая это, получим
(4.49)
где d у 1 = D S 1 /S 1, d у1 = D S 2 /S 2 - соответственно относительные мультипликативные погрешности преобразователей 1 и 2 (рис. 4.5).
Можно показать, что относительная аддитивная погрешность компенсационной схемы определяется таким же выражением (4.49) с той разницей, что d у 1, и d у 2 являются относительными аддитивными погрешностями.
По выражению (4.49) вычисляется погрешность схемы, если известны погрешности преобразователей 1 и 2. Если же эти погрешности являются случайными и известны их среднеквадратические погрешности s 1 и s 2, то среднеквадратическая погрешность компенсационного преобразователя
(4.50)
Из полученных соотношений следует, что влияние погрешности преобразователя 1 на погрешность прибора с компенсационной схемой сильно уменьшается.
Уменьшение зависимости погрешности прибора с обратной связью от погрешности преобразователя 1 можно показать следующим образом. Допустим, что в схеме сложного преобразователя с обратной связью (рис. 4.5) преобразователь 1 не стабилизирован и его чувствительность S1 может зависеть, в частности, от сопротивления, на которое нагружен этот сложный преобразователь. При уменьшении чувствительности S1 уменьшаются выходная величина у и сигнал обратной связи x ос. Это вызывает увеличение D х и увеличивает значение у. Таким образом, благодаря обратной связи уменьшается погрешность, вызванная изменением S1.
