Закодируем состояния каждого из элементов структурной схемы двоичными переменными: 1 (элемент исправный), 0 (элемент в отказовом состоянии). Тогда функционирование системы можно описать с помощью функций алгебры логики (ФАЛ), используя операции конъюнкции, дизъюнкции и инверсии. В качестве примера составим ФАЛ, соответствующую работоспособности системы с последовательным соединением элементов. Система находится в работоспособном состоянии при условии, что все ее элементы исправны. Обозначим xj — исправное состояние j -го элемента, 
— отказовое состояние, j = 1, 2,..., n. Тогда ФАЛ будет иметь вид:
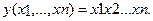
Рис. Структурные схемы нерезервированной (а) и резервированной (б) систем
Процедура получения ФАЛ может быть формализована. Одним из способов формализации является получение совершенной дизъюнктивной нормальной формы (СДНФ), получаемой из таблицы истинности, соответствующей работоспособному состоянию системы.
