Вероятность безотказной работы системы

Это вероятность того, что за заданное время t система не откажет.

 

Если элементы в системе соединены последовательно относительной надёжности, то выход из строя любого элемента выводит из строя всё систему

Структурная схема надежности имеет следующий вид:

 

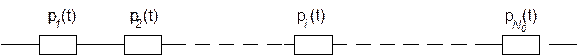
В этом случае в соответствии с теорией умножения вероятностей (вероятность умножения двух событий равна произведения вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место)

No p(t) = p1(t) * p2(t) * ……. * pi(t) * …… * pNo(t) = Пpi(t) i=1

(1.5)

В этом случае, если вероятность безотказной работы всех элементов системы равны.

p1(t) = p2(t) = …… = pi(t) = …… = pNo(t) =P(t)

 

No p(t) = [p(t)]

(1.6)

 

Так как вероятность p(t) < 1, то выражения 1.5 вытекает два важных вывода:

1)Надежность системы уменьшается при увеличении числа элементов

2)Вероятность безотказной работы системы всегда меньше вероятности безотказной работы самого надёжного элемента.

Вероятность отказа системы Q(t)

Это вероятность того, что за заданный интервал времени t в системе произойдет отказ, то есть время исправной работы Т будет меньше заданного.

 

Q(t) = 1 – p(t) = 1-p1(t) * p2(t) …… pi(t) …… pNo(t)

(1.7)

 

Q(t) = 1 –{[1-q1(t)] * [1-q2(t)] …… [1 – qi(t)] …. [1-qNo(t)]}

(1.8)

 

При одинаковой надёжности элементов:

 

No Q(t) = 1 – [1 –q(t)]

((1.9)

 

Если надёжность оценивается для малых промежутков времени, то вероятности отказов элементов, как правило <<1

qi(t) <<1

Тогда q_i(t)*q_i+t(t) в виду их малости в выражении 1.8 можно пренебречь, то 1.8 можно применить так

 

No Q(t) ≈ 1 – { 1- [q1(t) + q2(t) + …… + qi(t) + qNo(t)]} = ∑ qi(t) i=1

(1.10)

 

В том случае если вероятность отказов всех элементов равны, то 1.10 можно записать.

Q(t)≈ Noq(t)

(1.11)