В качестве примера рассмотрим основную эксплуатационную характеристику асинхронного электродвигателя – механическую ω (М), т.е. зависимость угловой скорости двигателя от его электромагнитного момента (рис. 12.2б).
На этой характеристике выделим два участка – рабочий 9-3 и нерабочий 3-6. На участке 9-3 двигатель работает устойчиво, на участке 3-6 – неустойчиво.
Вначале рассмотрим участок 9-3.
Пусть двигатель устойчиво работает в точке 4, т.е. со скоростью ω 
и электромагнитным моментом М = М 
.
Внесем в работу двигателя внешнее возмущение, а именно: с помощью сторонних (например, механических) сил разгоним двигатель до точки 7, после чего уберем эти силы при этом действие тормозного статического момента механизма М сохраняется.
Как после этого поведет себя двигатель?
Чтобы ответить на этот вопрос, надо сравнить величину двух моментов – вращающего электромагнитного двигателя М и тормозного статического момента механизма М .
Если в точке 4 оба момента были одинаковы (это обеспечивало установившийся режим работы привода с постоянной скоростью), то в точке 7 электромагнитный момент М двигателя уменьшился, а тормозной статический М не изменился.
В точке 7 тормозной момент М оказался больше вращающего М. В результате двигатель начнет тормозиться по участку 7-4, причем по мере приближения к точке 4 электромагнитный момент двигателя возрастает и в точке 4 снова уравняется со статическим. В точке 4 вновь наступит установившийся режим (М = М ).
Таким образом, на участке 4-7 двигатель, выведенный внешним возмущением из установившегося режима, вернулся в прежнее состояние после прекращения действия внешнего возмущения.
Значит, на участке 4-7 асинхронный двигатель работает устойчиво.
Рассуждая аналогично, можно показать, что так же устойчиво двигатель работает на участке 4-8. Если На этом участке сторонними силами тормозить ротор двигателя до точки 8, то момент двигателя М при скорости в точке 8 станет больше статического момента М . В результате, после прекращения действия внешнего возмущения, двигатель станет разгоняться и вернётся в точку 4. В точке 4 вновь наступит установившийся режим (М = М ).
Теперь рассмотрим работу двигателя на участке 3-6.
Пусть двигатель устойчиво работает в точке 1, т.е. со скоростью ω' и электромагнитным моментом М = М .
Внесем в работу двигателя внешнее возмущение, а именно: с помощью сторонних (например, механических) сил разгоним двигатель до точки 2, после чего уберем эти силы. Сравним в точке 2 величину двух моментов – вращающего электромагнитного двигателя М и тормозного статического момента механизма М .
В этой точке 2 электромагнитный момент М двигателя увеличился, а тормозной статический М не изменился. То есть, в точке 2 вращающий момент М оказался больше тормозного момента М . В результате двигатель начнет разгоняться по участку 2-3-8-4 до точки 4, в которой наступит установившийся режим (М = М ).
Таким образом, в результате действия внешнего возмущения двигатель не вернулся в старое, исходное состояние (точка 1), а перешел в новое установившееся состояние (точка 4).
Значит , работа двигателя на участке 1-3 – неустойчив а.
Рассуждая аналогично, можно показать, что так же не устойчиво двигатель работает на участке 1-6.
Если двигатель перевести из точки 1 в точку 5, принудительно затормозив ротор сторонними силами, то в точке 5 электромагнитный момент двигателя станет меньше статического. Поэтому, если убрать внешние силы, двигатель станет тормозиться и остановится в точке 6. В этой точке наступит установившийся режим стоянки под током.
Таким образом, в результате действия внешнего возмущения двигатель не вернулся в старое, исходное состояние (точка 1), а перешел в новое установившееся (точка 6).
Значит, работа двигателя на участке 1-6 – неустойчива.
Получим условие устойчивой и неустойчивой работы асинхронного двигателя.
На участке 9-3 (устойчивая работа) жесткость механической характеристики
β =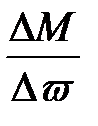 
< 0,
т.е. при увеличении момента М (ΔМ > 0), например, при переходе из точки 7 в точку 4, скорость падает (Δω < 0), и наоборот.
На участке 3-6 (неустойчивая работа) жесткость механической характеристики
β = 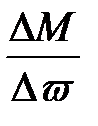> 0,
т.е. при увеличении момента М (ΔМ > 0), например, при переходе из точки 1 в точку 2 скорость также увеличивается, (Δω > 0), и наоборот.
Таким образом, двигатель работает устойчиво на участке механической характеристики, где жесткость отрицательна (β < 0) и неустойчиво на участке, где жесткость положительна (β > 0).
