Последовательность 
, первый член которой отличен от нуля и каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q, называется геометрической прогрессией. Число q - знаменатель прогрессии.
Называется n-ым членом последовательности
Формула n-го члена геометрической прогрессии имеет вид
Сумма бесконечной геометрической прогрессии:
| Определение геометрической прогрессии | bn+1 =bn · q, где bn ≠ 0, q ≠ 0 |
| Знаменатель геометрической прогрессии | 
|
| Формула n-го члена геометрической прогрессии | bn = b1 · q n-1 |
| Сумма n первых членов геометрической прогрессии |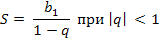  
|
Отношение любого члена геометрической прогрессии и ему предшествующего члена, равно одному и тому же числу q:
- Если
, то 
- монотонна - Если
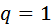, то - постоянна
Своё название прогрессия получила по своему характеристическому свойству:
то есть каждый член равен среднему геометрическому его соседей.
(РИТА К) Свойства:
1) Логарифмы членов геометрической прогрессии (если определены) образуют арифметическую прогрессию.
2) (Характеристическое свойство геометрической прогрессии). Квадрат n -го члена геометрической прогрессии равен произведению равноудаленных от него членов:
|
В частном случае, для трех последовательных членов геометрической прогрессии
|
3) Числа a, b, c (не обязательно в указанной очередности) образуют геометрическую прогрессию, если и только если удовлетворяют равенству
| (a 2 - bc)(b 2 - ac)(c 2 - ab) = 0, |
а числа a, b, c (в указанной очередности) образуют геометрическую прогрессию, если и только если
b 2 = ac.
4) Сумма S всех членов бесконечно убывающей геометрической прогрессии (| q | < 1) определяется по формуле
|
Доказательство:
· произведение первых n членов геометрической прогрессии можно рассчитать по формуле:
.
· Произведение членов геометрической прогрессии, начиная с k-ого члена, и заканчивая n-ым членом, можно рассчитать по формуле:
· Сумма 
первых членов геометрической прогрессии:
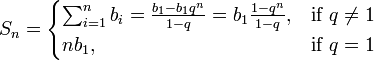
· Если 
, то 
при 
, и
при .
(ОЛЯ)Примеры:
ü Последовательность площадей квадратов, где каждый следующий квадрат получается соединением середин сторон предыдущего — бесконечная геометрическая прогрессия со знаменателем 1/2. Площади получающихся на каждом шаге треугольников также образуют бесконечную геометрическую прогрессию со знаменателем 1/2, сумма которой равна площади начального квадрата,
ü 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192 — прогрессия со знаменателем 2 из тринадцати членов.
ü 50; −25; 12,5; −6,25; 3,125; … — бесконечно убывающая прогрессия со знаменателем - 
.
1) Дана геометрическая прогрессия b1, b2, b3,..., bn,....
Известно, что b1 = 
, q = - 3. Найти b6
Решение. В этом случае в основе решения лежит формула n-го члена геометрической прогрессии.
Подставив в эту формулу n = 6 получим:
b6 = b1 · q5 = · (-3)5 = -162
Ответ -162.
2) Произведение первых трех членов геометрической прогрессии равно 1728, а их сумма равна 63. Найти первый член и знаменатель этой прогрессии.
Решение. Пусть b 1, b 2 и b 3- первые три члена данной прогрессии. Тогда из условия b 1 b 2 b 3 = 1728 следует 
и b 2 = 12. Следовательно,
Решения данной системы (см. обратную теорему Виета) является также корнями квадратного уравнения
z 2 - 51 z + 144 = 0.
Решая квадратное уравнение, получим 
= 3 и 
= 48, то есть, b 1 = 3, b 3 = 48 или b 1 = 48, b 3 = 3. Поскольку b 1 = 3, b 2 = 12 или b 1 = 48 и b 2 = 12, получим q = 4 или q = 1/4. Таким образом, решениями задачи будут 
= 3 и q = 4 или = 48 и q = 1/4.
(НАСТЯ)Задачи
1) Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м?
Решение: Составим математическую модель задачи: 1400, 1300, …, 1400-100(n-1). a1=1400; d=-100, Sn=5000.
Н! n. Sn= (2a1+ d (n-1))n:2;
5000= (2·1400-100 · (n-1)) n:2;
10000= (2800-100 n+100) n;
10000= (2900-100 n) n;
100 n2-2900 n+10000=0;
n2-29 n+100=0; n=25, n=4
По условию задачи удовлетворяет n=4 (при n=25 аn=-1000, но аn>0) Значит, альпинисты покорили высоту за 4 дня.
Ответ: за 4 дня.
(я)
2) Продавец киоска обратил внимание на то, что каждый год в последние 7 дней перед 8 марта количество продаваемых в день поздравительных открыток увеличивается в одно и тоже число раз по сравнению по сравнению с предыдущим днем. Начав торговлю открытками за 7 дней перед праздником, он подсчитал, что в третий день было продано 48 открыток, а в пятый день – 192 открытки. Сколько всего открыток будет продано за 7 дней торговли, если замеченная продавцом закономерность сохранится?
