2) Определить арифметическую прогрессию, если a 3 = 2 и a 5= -2.
Решение. Используя формулу общего члена арифметической прогрессии, получим систему
| a 3 = a 1+ 2 d, |
| a 5 = a 1+ 4 d, |
или, учитывая условия примера,
|
| a 1+ 2 d = 2, |
| a 1+ 4 d = -2, |
откуда находим первый член арифметической прогрессии 
= 6 и ее разность d = -2.
3) Определить сумму всех четных трехзначных чисел, делящихся на 3.
Решение. Первым четным трехзначным числом, делящимся на 3, является 102. Поскольку четное число, делящееся на 3, делится и на 6, получим прогрессию
102, 108, 114,..., 996,
где a 1 = 102, d = 6 и последний ее член ax = 996 (x 
N).
Поскольку ax = a 1 + (x - 1) d или
102 + (x - 1)·6 = 996,
находим x = 150. Тогда, используя формулу сумма первых n членов арифметической прогрессии, получим
4) Определить числа, являющиеся одновременно членами арифметической прогрессии, 2, 5, 8,..., 332 и 7, 12, 17,..., 157.
Решение. Пусть b - n -ый член первой прогрессии, следовательно,
b = 2 + (n - 1)·3 и, в то же время, b является m -ым членом во второй прогрессии, то есть, b = 7 + (m - 1)·5. Таким образом, получим уравнение
2 + (n - 1)·3 = 7 + (m - 1)·5,
или
3(n - 1) = 5 m
откуда, учитывая, что m, n - натуральные числа, получим n = 5 k + 1 и m = 3 k, k Î N, то есть, члены a 6, a 11, a 16,..., a 5 k +1 первой прогрессии совпадают с членами c 3, c 6, c 9,..., c 3 k, второй прогрессии. Таким образом, числа 17, 32, 47, 62, 77, 92, 107, 122, 137 и 152 входят в обе прогрессии.
Связь между арифметической и геометрической прогрессиями
Пусть 
— арифметическая прогрессия с разностью 
и число 
. Тогда последовательность вида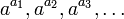 
есть геометрическая прогрессия со знаменателем 
.
