Для этого определим стандартное отклонение среднего арифметического 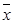 :
:
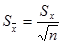 ;
;
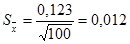
Т.к. закон распределения вероятности для среднего арифметического считаем нормальным, тогда доверительный интервал определится по выражению (значению доверительной вероятности 0.95 соответствует аргумент функции Лапласа t=1,8595):
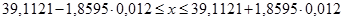
| 38,88322<X<39,34098 |
Как видно из сравнения результатов, неизвестность закона распределения вероятности приводит к расширению доверительного интервала, то есть к увеличению дефицита измерительной информации.
| интервалы | 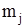
| 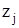
| 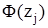
| 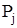
| mj – nPj | 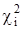
| ||
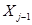
| 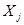
| |||||||
| 38,76 | 38,88 | -1,885677943 | 0,03005 | 0,02793 | 0,06 | 3,682366273 | ||
| 38,88 | 38,94 | -1,398212727 | 0,0968 | 0,06675 | 0,04 | 1,072003745 | ||
| 38,94 | 39,00 | -0,910747511 | 0,20897 | 0,11217 | 0,06 | 2,426414282 | ||
| 39,00 | 39,06 | -0,423282296 | 0,37448 | 0,16551 | 0,21 | 1,195915715 | ||
| 39,06 | 39,12 | 0,06418292 | 0,47608 | 0,1016 | 0,16 | 3,356850394 | ||
| 39,12 | 39,18 | 0,551648136 | 0,7088 | 0,23272 | 0,21 | 0,221810932 | ||
| 39,18 | 39,24 | 1,039113351 | 0,8508 | 0,142 | 0,09 | 1,904225352 | ||
| 39,24 | 39,30 | 1,526578567 | 0,936 | 0,0852 | 0,11 | 0,721877934 | ||
| 39,30 | 39,36 | 2,014043783 | 0,9778 | 0,0418 | 0,06 | 0,792440191 | ||
| 39.36 | 38,42 | -1,885677943 | 0,03005 | 0,02793 | 0,06 | 3,682366273 |
| i | Интервалы | mi | 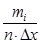
| 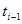
| 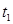
| Фi-1 | Фi | Pi | 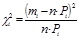
| ||
| xi-1 | xi | ||||||||||
| 37,31 | 37,42 | 0,6 | -2,15 | -1,56 | 0,00494 | 0,07215 | 0,067 | 0,077 | |||
| 37,42 | 37,52 | 1,3 | -1,56 | -1,03 | 0,07215 | 0,17619 | 0,104 | 0,648 | |||
| 37,52 | 37,62 | 1,7 | -1,03 | -0,49 | 0,17619 | 0,31207 | 0,136 | 0,857 | |||
| 37,62 | 37,72 | 1,6 | -0,49 | 0,05 | 0,31207 | 0,5199 | 0,208 | 1,1 | |||
| 37,72 | 37,82 | 2,1 | 0,05 | 0,58 | 0,5199 | 0,719 | 0,199 | 0,0597 | |||
| 37,82 | 37,92 | 1,3 | 0,58 | 1,12 | 0,719 | 0,8686 | 0,1496 | 0,257 | |||
| 37,92 | 38,02 | 0,8 | 1,12 | 1,66 | 0,8686 | 0,9515 | 0,083 | 0,01 | |||
| 38,02 | 38,12 | 0,5 | 1,66 | 2,19 | 0,9515 | 0,9857 | 0,0342 | 0,73 | |||
| 38,12 | 38,22 | 0,1 | 2,19 | 2,73 | 0,9857 | 0,9968 | 0,0111 | 0,011 | |||
ПРИМЕЧАНИЕ*






