Качественные показатели надежности указывают на то, что рассматриваемая система обладает каким-либо свойством, имеет то или иное устройство, способное выполнить поставленные задачи; дают возможность отличать системы друг от друга, но не позволяют сравнивать их по степени выполнения поставленной задачи, т.е. по надёжности.
Порядковые показатели надёжности дают возможность расположить в ряд по степени возрастания надежности, исследуемые варианты системы, но не позволяют оценить, на какую величину отличается достигнутый уровень надёжности рассматриваемых вариантов.
Количественные показатели надежности выражаются в виде числа, надежность измеряется или оценивается в принятой шкале оценок в абсолютных или относительных единицах при помощи этих показателей, количественные показатели определяются путем статических наблюдений на основе обработки результатов испытания или эксплуатации систем, а также путем аналитических расчетов или моделирования процессов функционирования систем. Они являются основными показателями надежности. Поэтому основное внимание уделим именно этим показателям.
Различают следующие типы показателей надежности:
Единичный показатель надежности – показатель надежности, характеризующий одно из свойств, составляющих надежность системы.
Комплексный показатель надежности - показатель надежности, характеризующий несколько свойств, составляющих надежность системы.
В отличие от единичного показателя надежности комплексный показатель надежности количественно характеризует не менее двух свойств, составляющих надежность, например безотказность и ремонтопригодность.
Расчетный показатель надежности – показатель надежности, значения которого определяются расчетным методом.
Экспериментальный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется по данным испытаний.
Эксплуатационный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется по данным эксплуатации.
Экстраполированный показатель надежности – показатель надежности, точечная или интервальная оценка которого определяется на основании результатов расчетов, испытаний и (или) эксплуатационных данных путем экстраполирования на другую продолжительность эксплуатации и другие условия эксплуатации.
Все показатели надежности в основном определяются как вероятностные характеристики. Это дает возможность прогнозирования значений этих показателей на этапе проектирования, при этом показатели надежности вводят по отношению к определенным режимам и условиям эксплуатации, установленным в НТД.
1.2.2.1 Функция надежности. Интегральный и дифференциальный законы распределения наработки до отказа. В [5] показано, что если рассмотреть систему, состоящую из двух элементов, состояние каждого из которых характеризуется одним основным параметром, то техническое состояние системы в целом можно рассматривать как точку с координатами 
на плоскости определяющих параметров. Будем считать, что система работоспособна, если оба ее определяющих параметров имеют значения, обеспечивающие функционирование системы, а область параметров 
, в которой система выполняет свои целевые функции, называют областью работоспособности (рис. 1.7).
Число параметров реальной системы велико, область параметров многомерно и состояние системы определяют как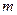 
-мерный вектор 
в пространстве параметров равных 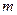. В общем случае область работоспособности многомерная криволинейная поверхность. Оперировать ими неудобно, поэтому в область работоспособности вписывают прямоугольную область допустимых параметров 
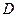. При этом условие работоспособности будет соответствовать отношению 
. Вероятность отсутствия отказа системы в фиксированный момент времени определиться по выражению
,
а вероятность отказа системы может быть записана как
.
Эти две вероятности характеризуют полную группу событий 
.
Рисунок 1.7 – Области работоспособности и допустимых значений
Функцией надежности называют функцию 
, выражающую вероятность того, что случайная наработка до отказа будет не менее заданной наработки, отсчитываемой от момента начала эксплуатации (рис. 1.8). Функция надежности обладает следующими свойствами:
- 
– в момент начала работы объект является безотказным;
- – монотонно убывающая функция заданной наработки (с течением времени вероятность отказа любого объекта возрастает;
- 
– любой объект со временем откажет.
Рисунок 1.8 – Зависимости функций надежности и ненадежности от наработки
Статистическую оценку функции надежности можно найти по выражению
где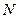 
– число однотипных изначально исправных объектов, поставленных на испытания;
– число исправных объектов в момент времени 
(неисправные объекты на исправные не заменяются).
Наряду с функцией надежности можно определить и обратную ей функцию ненадежности 
(см. рис. 1.8), которая имеет все признаки интегрального закона (
, 
– монотонно возрастает, 
), и называется интегральным законом распределения наработки до отказа.
Наряду с функцией надежности и интегральным законом распределения часто используют дифференциальный закон распределения наработки до отказа или плотность вероятности наработки до отказа:
.
Откуда
, 
.
Статистическую оценку плотности вероятности наработки до отказа найти по выражению
,
где 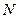– число однотипных изначально исправных объектов, поставленных на испытания;
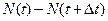– число отказавших объектов на интервале времени 
(неисправные объекты заменяются на исправные).
1.2.2.2 Показатели безотказности. Наиболее широкое применение получили следующие показатели безотказности:
- вероятность безотказной работы (ВБР) в течение определенного времени:
- гамма-процентная наработка до отказа;
- средняя наработка до отказа;
- параметр потока отказов;
- интенсивность отказов.
Вероятность безотказной работы – вероятность того, что в пределах заданной наработки отказ объекта не возникнет. Вероятность безотказной работы объекта в интервале 
определяют как
, (1.1)
где – случайная наработка до отказа;
– заданная наработка объекта;
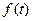– плотность вероятности наработки до отказа.
Вероятность безотказной работы является функцией наработки . Обычно эту функцию предполагают непрерывной и дифференцируемой. Если способность объекта выполнять заданные функции характеризуется одним параметром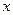 
, то вместо (1.2) имеем формулу
,
где 
и 
- предельные по условиям работоспособности значения параметров (эти значения, вообще, могут изменяться во времени).
Аналогично вводят ВБР в более общем случае, когда состояние объекта характеризуется набором параметров с допустимой по условиям работоспособности областью значений этих параметров.
Точечные статистические оценки для вероятности безотказной работы 
для функции распределения наработки до отказа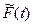 
определяются формулами:
; 
,
где 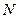– число объектов, работоспособных в начальный момент времени;
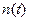– число объектов, отказавших на отрезке времени 
.
Для получения достоверных оценок объем выборки 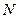должен быть достаточно велик.
Определение безотказной работы в соответствии с формулой (1.1) относится к объектам, которые должны функционировать в течение некоторого конечного отрезка времени. Для объектов одноразового (дискретного) применения ВБР определяют как вероятность того, что при срабатывании объекта отказ не возникает. Аналогично вводят вероятность безотказного включения (например, в рабочий режим из режима ожидания).
Гамма-процентная наработка до отказа – наработка, в течение которой отказ объекта не возникает с вероятностью 
, выраженной в процентах. Данный показатель определяют по формуле:
, (1.2)
где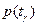 
– вероятность безотказной работы;
– функция распределения наработки до отказа в момент времени 
.
Как видно из формулы (1.5), гамма-процентные показатели равны квантилям соответствующих распределений. Если вероятности, отвечающие этим квантилям, выражают в процентах, то для показателей безотказности обычно задают значения 90; 95; 99; 99,5 % и т.д. Тогда вероятности возникновения отказа на отрезке будут соответственно составлять 0,10; 0,05; 0,01; 0,005 и т.д. Задаваемые значения для критических отказов должны быть весьма близки к 100%, чтобы сделать критические отказы практически невозможными событиями. Для прогнозирования потребности в запасных частях, инструментах и принадлежностях (ЗИП), а также для расчета его пополнения могут потребоваться гамма-процентные показатели при более низких значениях , например, при 
. Статистические оценки для гамма-процентных показателей могут быть получены на основе статистических оценок либо непосредственно, либо после аппроксимации эмпирических функций подходящими аналитическими распределениями. Необходимо иметь в виду, что экстраполирование эмпирических результатов за пределы продолжительности испытаний (наблюдений) без привлечения дополнительной информации о физической природе отказов может привести к значительным ошибкам. При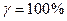 
, гамма-процентная наработка называется установленной безотказной наработкой, а при – медианной наработкой.
Средняя наработка до отказа – математическое ожидание наработки объекта отказа. Среднюю наработку до отказа 
вычисляют по формуле
, (1.3)
где – функция распределения наработки до отказа,
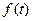– плотность распределения наработки до отказа.
С учетом (1.1) выражается через вероятность безотказной работы:
.
Статистическая оценка для средней наработки до отказа определяется по выражению
,
где 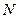- число работоспособных объектов при 
,
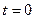- наработка до первого отказа каждого из объектов.
Средняя наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течение этой наработки.
Этот показатель введен применительно к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Очевидно, что это должны быть несуществующие отказы, не приводящие к серьезным последствиям и не требующие значительных затрат на восстановление работоспособного состояния. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работать и продолжает работать до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т. д. На оси времени моменты отказов образуют поток отказов, а моменты восстановлений - поток восстановлений. На оси суммарной наработки (когда время восстановления не учитывается) моменты отказов образуют поток отказов. Полное и строгое математическое описание эксплуатации объектов по этой схеме построено на основе теории восстановления.
Интенсивность отказов – условная плотность вероятности возникновения отказа объекта, определяемая для рассматриваемой наработки при условии, что до рассматриваемого момента времени отказ не возник. Интенсивность отказов 
определяют по формуле
Интенсивность отказов определяют по формуле
. (1.4)
Статистическая оценка для интенсивности отказов 
имеет вид
,
где 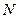– число объектов, работоспособных в начальный момент времени ;
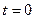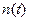– число объектов, отказавших на отрезке ;
– число объектов, отказавших на отрезке 
;
Аналогично вводится интенсивность восстановления.
Все показатели безотказности определены как вероятностные характеристики. Их статистические аналоги определяют методами математической статистики.
1.2.2.3 Показатели долговечности, ремонтопригодности и сохраняемости. К показателям ремонтопригодности относятся:
- вероятность восстановления – вероятность того, что время восстановления работоспособного состояния объекта не превысит заданное значение;
- гамма-процентное время восстановления – время, в течение которого восстановление работоспособности объекта будет осуществлено с вероятностью , выраженной в процентах;
- среднее время восстановления – математическое ожидание времени восстановления работоспособного состояния объекта после отказа;
- интенсивность восстановления – условная плотность вероятности восстановления работоспособного состояния объекта, определенная для рассматриваемого момента времени при условии, что до этого момента восстановление не было завершено;
- средняя трудоемкость восстановления – математическое ожидание трудоемкости восстановления объекта после отказа.
Вероятность восстановления определяется по выражению
,
где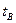 
– случайное время восстановления;
– заданное время восстановления;
– плотность вероятности длительности восстановления.
Среднее время восстановления определяется по выражению
.
Параметр потока восстановления – интенсивность восстановления 
определяется аналогично интенсивности отказов .
К показателям сохраняемости относятся:
- гамма-процентный срок сохраняемости – срок сохраняемости, достигаемой объектом с заданной вероятностью , выраженной в процентах;
- средний срок сохраняемости – математическое ожидание срока сохраняемости.
К показателям долговечности относятся:
- гамма-процентный ресурс – суммарная наработка, в течение которой объект не достигнет предельного состояния с вероятностью γ, выраженный в процентах;
- средний ресурс – математическое ожидание ресурса;
- гамма-процентный срок службы – календарная продолжительность эксплуатации, в течение которой объект не достигает предельного состояния с вероятностью , выраженной в процентах;
- средний срок службы – математическое ожидание срока службы.
При использовании показателей долговечности следует указывать начало отсчета и вид действий после наступления предельного состояния (например, гамма-процентный ресурс от второго капитального ремонта до списания). Показатели долговечности, отсчитываемые от ввода объекта в эксплуатацию до окончательного снятия с эксплуатации, называются гамма-процентный полный ресурс (срок службы), средний полный ресурс (срок службы).
1.2.2.4 Комплексные показатели надежности. Комплексным показателем надежности объекта, характеризующим его безотказность и ремонтопригодность является коэффициент готовности. Коэффициент готовности – вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени, кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается.
Различают стационарный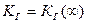 
и нестационарный коэффициенты готовности 
.
Коэффициент готовности характеризует готовность объекта к применению по назначению только в отношении его работоспособности в произвольный момент времени.
Cтационарный коэффициент готовности (предельное значение коэффициента готовности) 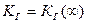определяется по формуле
.
где – средняя наработка на отказ;
– среднее время восстановления.
Наряду с коэффициентом готовности часто используется такой показатель как коэффициент простоя – вероятность застать систему в неисправном состоянии
;
.
Для одного ремонтируемого объекта стационарный коэффициент готовности можно определить по выражению
,
где 
– время сохранения работоспособности в 
-м цикле функционирования объекта; 
– время восстановления (ремонта) после -го отказа объекта.
Коэффициент готовности показывает какую часть времени объект находится в работоспособном состоянии.
Коэффициент технического использования – отклонение математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за этот период.
Коэффициент технического использования равен отношению математического ожидания суммарного времени пребывания объекта в работоспособном состоянии за некоторый период эксплуатации к математическому ожиданию суммарного времени пребывания объекта в работоспособном состоянии и простоев, обусловленных техническим обслуживанием и ремонтом за тот же период эксплуатации:
,
где 
– средняя длительность ТО.
Для одного ремонтируемого объекта коэффициент использования можно определить по выражению
,
где – время сохранения работоспособности в -м цикле функционирования объекта;
– время восстановления (ремонта) после -го отказа объекта;
– длительность выполнения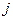 
-го ТО (профилактики), требующего вывода объекта из работающего состояния (использования по назначению);
– число рабочих циклов за рассматриваемый период эксплуатации;
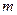– число отказов (восстановлений) за рассматриваемый период;
– число профилактик, требующих отключения объекта в рассматриваемый период.
Коэффициент технического использования характеризует долю времени нахождения объекта в работоспособном состоянии относительно общей продолжительности эксплуатации.
Коэффициент оперативной готовности – вероятность того, что объект окажется в работоспособном состоянии в произвольный момент времени кроме планируемых периодов, в течение которых применение объекта по назначению не предусматривается, и, начиная с этого момента, будет работать безотказно в течение заданного интервала времени.
Из вероятностного определения следует, что
,
где – вероятность безотказной работы объекта в течение времени , необходимого для безотказного использования по назначению.
Коэффициент оперативной готовности характеризует надежность объекта, необходимость применения которого возникает в произвольный момент времени, после которого требуется безотказная работа в течение заданного интервала времени.
Коэффициент сохранения эффективности – отношение значения показателя эффективности использования объекта по назначению за определенную продолжительность эксплуатации к номинальному значению этого показателя, вычисленному при условии, что отказы объекта в течение того же периода не возникают.
Коэффициент сохранения эффективности может быть определен по выражению
,
где 
, 
– показатели реальной и номинальной эффективности объекта.
