Многократное измерение одной и той же величины постоянного размера производится при повышенных требованиях к точности измерений. Такие измерения характерны для профессиональной метрологической деятельности и при выполнении точных научных экспериментов.
Результатом многократного измерения величины X является интервал её возможных значений 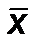 -
-  , где
, где 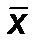 – среднее значение многократно измеренной величины,
– среднее значение многократно измеренной величины,  – случайная погрешность измерения.
– случайная погрешность измерения.
Многократное измерение начинается с тщательного анализа предварительной информации. В ходе этого анализа уясняется физическая сущность изучаемого явления, уточняется его модель, определяются влияющие факторы и меры, направленные на уменьшение их влияния (например, компенсация электрических и магнитных полей), значения поправок. Также принимается решение в пользу той или иной методики измерения, выбирается средство измерений, изучаются его метрологические характеристики и опыт выполнения подобных измерений в прошлом. Важным итогом этой работы должна стать твёрдая уверенность в том, что необходимая точность достигнута и она достаточна. Если это условие выполняется, то после необходимых приготовлений, включающих установку и подготовку к работе средства измерений, исключение или компенсацию влияющих факторов, выполняется получение значений многократно измеряемой величины.
Обработка ряда значений  , полученных путём многократных равноточных измерений (т.е. измерений одной и той же величины, выполненных с одинаковой точностью, одним и тем же средством измерения, в одинаковых условиях, одним исследователем) величины выглядит так:
, полученных путём многократных равноточных измерений (т.е. измерений одной и той же величины, выполненных с одинаковой точностью, одним и тем же средством измерения, в одинаковых условиях, одним исследователем) величины выглядит так:
1. Используя полученные данные, находят среднее значение величины 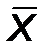 .
.
2. Вычисляют оценку СКО (среднее квадратическое отклонение) среднего значения величины.
3. При заданной доверительной вероятности P и числе полученных значений n по табл. 1 определяют коэффициент Стьюдента 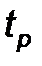 , с помощью которого находят границы доверительного интервала для случайной погрешности.
, с помощью которого находят границы доверительного интервала для случайной погрешности.
4. Записывают интервал возможных значений измеряемой величины 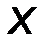 .
.
Таблица 1 – Значения коэффициента Стьюдента 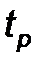
| Число измерений, n | Число степеней свободы, k = n - 1 | Доверительная вероятность, P | ||
| 0,90 | 0,95 | 0,99 | ||
| 6,31 | 12,71 | 63,68 | ||
| 2,92 | 4,30 | 9,93 | ||
| 2,35 | 3,18 | 5,84 | ||
| 2,13 | 2,78 | 4,60 | ||
| 2,02 | 2,57 | 4,06 | ||
| 1,94 | 2,45 | 3,71 | ||
| 1,90 | 2,37 | 3,50 | ||
| 1,86 | 2,31 | 3,36 | ||
| 1,83 | 2,26 | 3,25 | ||
| 1,81 | 2,23 | 3,17 | ||
| 1,80 | 2,20 | 3,11 | ||
| 1,78 | 2,18 | 3,06 | ||
| 1,77 | 2,16 | 3,01 | ||
| 1,76 | 2,15 | 2,98 |
При оценивании границ доверительного интервала случайной погрешности обычно принимают вероятность, равную 0,90, 0,95 или 0,99. Использование других вероятностей должно быть обосновано.






