Формы представления погрешностей измерений, при установлении классов точности

Форма представления класса точности средства измерений, определяется пределами допускаемой основной погрешности измерений. В ряде случаев вместе с основной нормируются пределы допускаемой дополнительной погрешности.

Пределы допускаемых погрешностей измерений выражаются границами (верхней и нижней) абсолютной погрешности средства измерений.

Сама форма представления класса точности пределами допускаемой основной абсолютной погрешности применяется преимущественно для мер массы или длины, которые принято выражать в единицах массы или длины. Класс точности измерительных приборов в большинстве случаев выражается пределами допускаемой основной приведенной или относительной погрешности. При этом основой для определения формы представления класса точности прибора является характер изменения основной абсолютной погрешности средства измерений.

1. Если основная абсолютная погрешность имеет аддитивный характер, т. е. границы погрешностей измерительного прибора не изменяются в пределах диапазона измерений, то класс точности представляется пределами допускаемой приведенной погрешности (формула 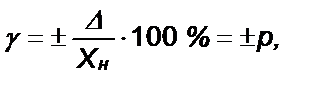1).

(1)

где D = ± а – пределы допускаемой основной абсолютной погрешности прибора; р – отвлеченное положительное число, выбираемое из ряда чисел, указанных ниже; X_н – нормирующее значение средства измерений.

2. Если основная абсолютная погрешность имеет мультипликативный характер, т. е. границы погрешностей измерительного прибора линейно изменяются в пределах диапазона измерений,то класс точности представляется пределами допускаемой относительной погрешности δ в виде (формула 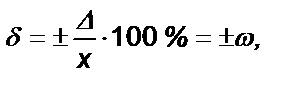2):

(2)

где Δ = ± bx – пределы допускаемой абсолютной погрешности прибора; X – показания прибора; ω – отвлеченное положительное число.

3. Если основная абсолютная погрешность имеет и аддитивную, и мультипликативную составляющие, то класс точности представляется пределами допускаемой относительной погрешности d в виде (формула 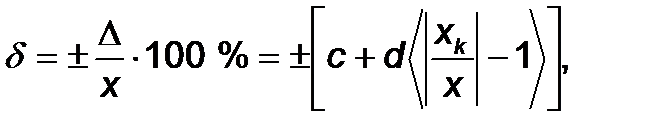3):

(3)

где (а + bх), с и d – отвлеченные положительные числа.

Положительные числа р, w, с, d выбираются из установленного ряда: 1×10ⁿ; 1,5×10ⁿ; 2,0×10ⁿ; 2,5×10ⁿ; 4×10ⁿ; 5×10ⁿ; 6×10ⁿ; (n = 1; 0; -1; -2;
-3 и т.д.).

Для некоторых СИ характерна сложная зависимость относительной погрешности от измеряемой величины или влияющих факторов, которая приводит к логарифмической характеристике точности. В основном это широкодиапазонные СИ, например мосты сопротивлений, цифровые частотомеры и.т.п.