Для оценки надежности таких объектов применяются количественные показатели отдельных свойств. Эти показатели позволяют проводить расчетно-аналитическую оценку количественных характеристик отдельных свойств с целью выбора различных схемных и конструктивных вариантов оборудования (объектов), при проектировании, испытаниях и в условиях эксплуатации.
Показатели надежности – это количественная характеристика одного или нескольких свойств, составляющих надежность объекта. Если показатель надежности характеризует одно из свойств надежности, то он называется единичный, если же несколько свойств – комплексным показателем надежности. В основе большинства показателей надежности лежат оценки наработки, т.е. продолжительности объема работы, выполненной объектом. Когда система работает с перерывами, учитывается суммарная наработка. Если объект эксплуатируется в различных режимах, влияющих на показатели надежности, то наработки могут суммироваться для каждого режима отдельно. Рассмотрим показатели надежности, рекомендуемые нормативными документами [20,2].
На стадиях экспериментальной отработки, испытаний и эксплуатации, роль показателей надежности выполняют статистические оценки соответствующих вероятностных характеристик. К основным показателям надежности невосстанавливаемых объектов относятся: P (t); Q(t); a(t); λ(t); T.
Вероятность безотказной работы P (t) – вероятность того, что в течение рассматриваемого промежутка времени (0, t) в системе или элементе не произойдет отказ.
Статистически P (t) определяется как отношение числа элементов 
, безотказно проработавших до момента t, к первоначальному числу элементов, поставленных на испытание N 0:
(2.1)
где n (t) – число отказавших за время (0, t) элементов, следовательно
, 
, 
. (2.2)
Например, на испытания поставлено 1000 образцов однотипных реле, то есть N 0 = 1000 реле. При испытании отказавшие реле не заменялись исправными. За время t отказало 10 реле. Следовательно, P (t) = 0,99, поэтому любое реле из данной испытуемой выборки не откажет за время t с вероятностью P (t) = 0,99.
Иногда целесообразно пользоваться не вероятностью безотказной работы, а вероятностью отказа Q(t).
Вероятность появления отказаQ(t) −вероятность того, что в заданном интервале времени (0, t) произойдет отказ.
Поскольку работоспособность и отказ являются состояниями несовместными и противоположными, то их вероятности связаны зависимостью:
, (2.3)
тогда:
. (2.4)
Статистическая оценка вероятности отказа Q (t)
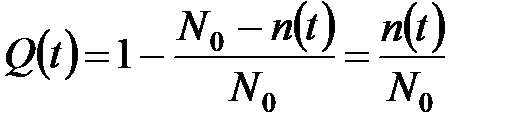. (2.5)
Частотой отказов называется отношение числа отказавших элементов системы в единицу времени к числу элементов, первоначально установленных на испытание при условии, что отказавшие элементы не восстанавливаются и не заменяются исправным.
Статистическая оценка a (t):
(2.6)
где n (t, 
t) – число элементов, отказавших в интервале времени от t до t+ t.
Интенсивностью отказов – это есть отношение числа отказавших элементов системы в единицу времени к среднему числу элементов, исправно работающих в данный отрезок времени при условии, что отказавшие элементы не восстанавливаются и не заменяются исправными. Таким образом, 
представляет собой относительную скорость появления отказа [ 7].
Статистическая оценка интенсивности отказов имеет вид:
, (2.7)
где 
- число отказавших элементов в интервале (
); 
- среднее число исправно работающих элементов в интервале 
; 
- интервал времени;
,
где Ni − число работоспособных объектов в начале интервала ; 
− число работоспособных объектов в конце интервала (рис. 2.1.).
Различие между частотой и интенсивностью отказов в том, что первый показатель характеризует вероятность отказа элемента за интервал 
, взятого из группы элементов произвольным образом, причем неизвестно, в каком состоянии (работоспособном или неработоспособном) находится выбранный элемент. Второй показатель характеризует вероятность отказа элемента за тот же интервал времени, взятого из группы элементов, оставшихся работоспособными, к моменту времени t.
| Рис. 2.1. Схема для определения N ср |
| N (Δ ti) |
| Ni |
| Ni+ 1 |
| Nср |
| Δ ti |
| t |
| Ni |
. Поэтому в практических расчетах возможна их замена.
Одним из основных понятий теории надежности является понятие «наработка», так как отказы и переходы в предельное состояние объектов обусловлены их работой.
Наработка до отказа – это наработка объекта от начала эксплуатации до возникновения первого отказа и измеряется в единицах времени. Средней наработкой до отказа (среднее время безотказной работы) называется математическое ожидание наработки объекта до первого отказа T
. (2.8)
Этот показатель относится и к восстанавливаемым объектам, при эксплуатации которых допускаются многократно повторяющиеся отказы. Эксплуатация таких объектов может быть описана следующим образом: в начальный момент времени объект начинает работу и продолжает работу до первого отказа; после отказа происходит восстановление работоспособности, и объект вновь работает до отказа и т.д.
Средняя наработка на отказ объекта (наработка на отказ) определяется как отношение суммарной наработки восстанавливаемого объекта к числу отказов, происшедших за суммарную наработку:
, (2.9)
где 
−наработка между отказами, ч; 
−суммарное число отказов за время 
.
Для статической оценки величины Т применяется формула:
(2.10)
где N 0 − число работоспособных однотипных невосстанавливаемых объектов при t = 0 (в начале испытания); ti − время безотказной работы i -го элемента.
Частота отказов, вероятность безотказной работы и вероятность появления отказа связаны следующими зависимостями:
; (2.11)
. (2.12)
Частота отказов, являясь плотностью распределения, наиболее полно характеризует такое случайное явление, как время возникновения отказов. Вероятность безотказной работы, математическое ожидание, дисперсия и т. п. являются лишь удобными характеристиками распределения и всегда могут быть получены, если известна частота отказов a (t). Вэтом ее основное достоинство как характеристики надежности [17].
Частота отказов a (t) – это естьпроизводная от вероятности появления отказа, означающая вероятность того, что отказ элемента произойдет за единицу времени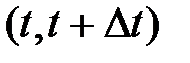 
.
. (2.13)
Интенсивность отказов 
− условная вероятность отказа после момента t за единицу времени 
при условии, что до момента t отказа элемента не было. Интенсивность отказов связана с частотой отказов и вероятностью безотказной работы:
. (2.14)
