4.8.1 Вычисление стандартной неопределенности по типу А -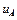 
4.8.1.1 Исходными данными для вычисления 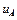являются результаты многократных измерений: xi 1, …, 
(где i = 1, …; m; 
- число измерений i -й входной величины).
4.8.1.2 Стандартную неопределенность единичного измерения i -й входной величины 
вычисляют по формуле
, (4)
где 
- среднее арифметическое результатов измерений i -й входной величины.
4.8.1.3 Стандартную неопределенность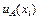 
измерений i -й входной величины, при которых результат определяют как среднее арифметическое, вычисляют по формуле
. (5)
4.8.2 Вычисление стандартной неопределенности по типу В – 
4.8.2.1 В качестве исходных данных для вычисления 
используют:
- данные предшествовавших измерений величин, входящих в уравнение измерения; сведения о виде распределения вероятностей;
- данные, основанные на опыте исследователя или общих знаниях о поведении и свойствах соответствующих приборов и материалов;
- неопределенности констант и справочных данных;
- данные поверки, калибровки, сведения изготовителя о приборе и т.п.
4.8.2.2 Неопределенности этих данных обычно представляют в виде границ отклонения значения величины от ее оценки. Наиболее распространенный способ формализации неполного знания о значении величины заключается в постулировании равномерного закона распределения возможных значений этой величины в указанных (нижней и верхней) границах [ 
для i -й входной величины]. При этом стандартную неопределенность, вычисляемую по типу В - 
, определяют по формуле
, (6)
а для симметричных границ 
- по формуле
. (7)
4.8.2.3 В случае других законов распределения формулы для вычисления неопределенности по типу В будут иными.
4.8.3 Для вычисления коэффициента корреляции 
используют согласованные пары измерений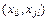 
(где l = 1; …, 
- число согласованных пар результатов измерений)
. (8)
4.9 Вычисление суммарной стандартной неопределенности 
4.9.1 В случае некоррелированных оценок 
, суммарную стандартную неопределенность 
вычисляют по формуле
. (9)
4.9.2 В случае коррелированных оценок суммарную стандартную неопределенность вычисляют по формуле
, (10)
где 
- коэффициент корреляции;
- стандартная неопределенность i -й входной величины, вычисленная по типу А или В.
