Математическое понятие динамической (причинной) системы служит для описания потока причинно-следственных связей из прошлого в будущее.
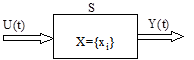Определение. Динамической системой S называется восьмёрка множеств
S = (T, X, U, Ω, Y, Г, ϕ, η),
где
· T – множество моментов времени как упорядоченное подмножество множества вещественных чисел;
· X – множество переменных состояния системы (множество состояний);
· U – множество мгновенных значений входных воздействий;
· Ω – множество допустимых входных воздействий Ω={ω: T →U}, которое удовлетворяет условиям нетривиальности (Ω не равно 0) и сочленения входных воздействий на заданном отрезке;
· Y – множество мгновенных значений выходных величин;
· Г – множество допустимых выходных величин Г;
· ϕ – переходная функция состояния ϕ: T х T х X х Ω → X, значениями которой служат состояния x(t2)=ϕ(t2; t1, x(t1), ω)∈X, в которых оказывается система в момент времени t2∈T, если в начальный момент времени t1∈T она была в начальном состоянии x(t1) ∈ X и если на неё действовало входное воздействие ω(t1,t2) ∈ Ω⊂U. При этом ϕ обладает свойством направленности времени, согласованности, сочленения и причинности.
· η – функция наблюдения η (выходное отображение): ТxX→Y, определяющая выходные величины y(t)=η[t,x(t)].
Данное понятие динамической системы является достаточно общим для того, чтобы выработать общую терминологию, но недостаточно конкретно, чтобы получать новые математические результаты.
Упрощённым вариантом описания динамической системы является описание системы в виде черного ящика (“вход - выход”):
S: Ω x Г, или S: U x Y, или S: Ω xY.
Модель функционирования системы в виде “чёрного ящика” отображает только связи системы с внешней средой в виде перечня “входов” и “выходов”.
Примеры описания динамических систем.
1. Модель нелинейной системы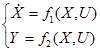 
2. Модель линейной системы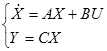 
, где А, В, С – числовые матрицы
3. В операторной форме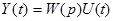 
, где р – оператор дифференцирования
