Процесс (лат. processus – продвижение) – последовательная смена во времени явлений, событий, состояний, либо множество последовательных действий, направленных на достижение какого – либо конечного результата (цели).
Переменные (координаты) процесса – это наиболее существенные параметры, характеризующие состояние процесса и изменяющие свои значения во времени: { xi(t) } = X(t).
Состояние процесса в момент времени tk - это множество значений переменных в этот момент времени: {xi(tk)}, где tk ∈T, T – множество моментов времени
В каждый момент времени t∈T система S получает некоторое множество входных воздействий U(t) и порождает некоторую выходную величину Y(t). В общем случае значение выходной величины системы зависит как от текущего значения входного воздействия, так и от предыстории этого воздействия. (Например, система в момент воздействия была или в состоянии покоя, или же находилась в движении из–за действия предыдущих входных величин). Чтобы не различать эти два случая, лучше говорить, что текущее значение выходной величины y(t) системы S зависит от состояния системы. Состояние системы описывается системой уравнений
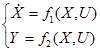
Состояние системы – это есть некоторая (внутренняя) характеристика системы {xi}, значение которой в настоящий момент времени определяет текущее значение выходной величины {Yj} и оказывает влияние на её будущее.
T x X → Y.
При этом знание состояния x(t₁) и отрезка входных воздействий ω=ω(t₁,t₂) должно быть необходимым и достаточным условием, позволяющим определить состояние x(t₂) = ϕ(t₂;t₁,x(t₁),ω) каждый раз, когда t₁<t₂. При этом множество Т упорядочено, т.е. в нём определено направление. Обычно направление Т таково, что прошлое предшествует будущему и влияет на него, но не наоборот.
Пара (τ, x), где τ∈Т и x∈X называется событием /фазой/ системы.
Множество T х X – пространство событий /фазовое пространство/ системы.
Иногда фазовое пространство называется пространством состояний. Переходная функция состоянийϕ (её график в пространстве событий) называется несколькими эквивалентными терминами: движением, траекторией, орбитой, потоком, решением дифференциального уравнения, кривой решения и т.д. Говорят, что входное воздействие (или управление ω) переводит (переносит, изменяет, преобразует) состояние x(t1) /или событие (t1, x)/ в состояние x(t2) = j(t2; t1, x(t1), ω) /или в событие (t2,ϕ(t2; t1, x(t1), ω)) /. Говоря о движении системы S, имеют в виду функцию состояния ϕ.
