Конкретные примеры влияния различных факторов на возникновение погрешностей измерения

 

Влияние особенностей конструкций СИ (рис.11,12).

 

Например, в конструкции штангенциркуля не соблюдается принцип компарации – принцип совпадений (Аббе), т.к. ось (линия) измерения не совпадает с осью шкалы, т.е. одна ось не является продолжением другой, а являются номинально параллельными. При этом они имеют отклонение от параллельности. Между осями образуется некоторый угол α.

ось шкалы

 

 

реальное расположение губок

 

h

 

α

ось измерения

 

Δ Δ

теоретическое расположение губок

Δ = h _* tgα» h _* α; 2Δ=h _* 2tgα» h _* 2α

 

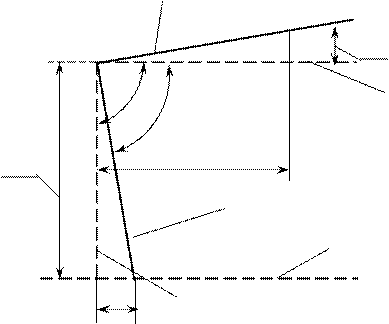
Рис.11 Схема особенностей конструкции штангенциркуля

 

 

Чем большим будет расстояние между осями h, тем большей будет погрешность измерения.

Кроме того, между штангой и рамкой штангенциркуля обязательно должен быть конструктивный зазор. В противном случае нельзя будет перемещать рамку с подвижной губкой по штанге.

Примем, например, номинальный зазор s_ном = 0,01 мм, расстояние от штанги до линии измерения L = 40 мм, измеряемый размер l = 10 мм.

 

Реальное расположение рамки

 

S_ном

 

штанга (теортическое

расположение рамки

или ось основной шкалы)

L l

 

реальное расположение подвижной губки

 

линия измерения

 

Δ теоретическое расположение подвижной губки

 

 

Рис.12 Схема размещения конструктивного зазора

 

Δ = S_{ном *} L / l = 0,01 _* 40 / 10 = 0.4 /10 = 0,04 мм.

Это без учета погрешности самого зазора, отклонения от перпендикулярности губки к штанге, деформации губок от натяга, отклонений формы и расположения штанги и рамки.

Влияние определения доли шкалы деления на глаз.

Δ = 0,2 _* i, где i – цена деления нониуса. Для гладкого микрометра i = 0,01 мм. Тогда Δ = 0,2 _* i = 0,2 _* 0,01 = 0,002 мм, т.е. долю деления шкалы нониуса не имеет смысла определять.

Влияние отклонений формы и расположения деталей СИ (рис. 13,14)

Рассмотрим, например, измерение при помощи гладкого микрометра. В зависимости от расположения точек контакта на измерительных поверхностях, отклонения от параллельности их могут полностью войти в погрешность измерения: Δ = b = a. Из-за несовпадения (перекоса) осей измерительных стержней появляется дополнительная погрешность.

 

a

 

b

 

Рис.13 Схема отклонений от параллельности измерительных поверхностей

 

l₁

 

α

 

l₂

 

Δ = l₂ – l₁

 

 

Рис.14 Схема перекоса измерительных стержней

 

Это не считая смещения осей от номинального положения (позиционных отклонений осей) и отклонения от соосности.

 

Влияние отклонения от соосности a ценров центровых бабок при измерении радиального биения (рис.15)

2

 

γ Δr_y a

 

L₁

L

 

 

Рис.15 Схема отклонений от соосности центров центровых бабок

Ось объекта измерения поворачивается на угол γ = arctg a/L₁, где L₁ – расстояние от центра 1 до плоскости измерения. Из-за угла γ возникает погрешность измерения Δr_y в определении r_y объекта, т.е. радиального биения: Δr_y = (L₁ / L) _* a. Если принять а = 0,01 мм, L = 500 мм, L₁ =450 мм, то Δr_y = (450 / 500) _* 0,01 = 0,9 _* 0,01 = 0,009 мм.

 

Влияние первичной погрешности нанесения шкалы (рис.16).

 

Под погрешностью нанесения шкалы понимают неточность положения любой ее отметки относительно нулевой. Первичной погрешностью нанесения шкалы называют накопленную погрешность от длины деления.

а а – длина деления (мм),

L – длина шкалы (мм).

 

L

 

Рис.16 Схема определения первичной погрешности нанесения шкалы

 

Обычно, для серийновыпускаемых СИ имеет место зависимость:

Δ = ± (0,5 + L / 100) мкм.

Если принять а = 1 мм, L = 100 мм, то

Δ = ± (0,5 + 100 / 100) = ± 1,5 мкм,

если L = 200 мм, то Δ = ± 2,5 мкм.

Это погрешность только от неточности длины деления. Но имеют место еще неточность толщины отметки, отклонение отметок от перпендикулярности к оси шкалы, отклонение оси от ее номинального направления, неточность калибровки. Например, обычно, погрешность калибровки шкал составляет 0,1 мкм.

Влияние неточности блока концевых мер длины

 

Например, если блок с номинальным размером 88,625 мм составлен из 4-х мер первого класса точности. В него войдут меры: 1,005; 1,12; 6,5; 80 мм. Только погрешность измерения мер составит:

Это без учета погрешностей от их притирания и калибровки. Погрешность калибровки каждой из мер будет меньше указанных погрешностей, погрешность калибровки всего блока (притертого) будет еще меньше (погрешность калибровки блока в целом будет меньше суммарной погрешности калибровки каждой из мер, входящих в блок). Если учесть еще и погрешность от притирания, то с учетом зазоров (без учета калибровки) получим:

Δ_Σ + 0,075 _* 3 = ± 0,6 + 0,225 = ± 0,825 мкм

(0,075 мкм – средняя погрешность на каждом из трех зазоров). Это без учета погрешностей боковичков, базовых поверхностей державки и от усилия зажима.

 

Влияние усилия сжатия блока концевых мер при установке на размер, например, индикаторного нутромера

 

Часто винт струбцины (державки) зажимают воротком или отверткой. При этом усилие сжатия блока доходит до 2000 Н (200 кгс), что приводит к деформациям, которые можно рассчитать по формуле: Δl = F _* l / S _* E, где F – сила сжатия (Н), l – размер блока (см), S – опорная площадь меры (см²), E – модуль упругости (Н/ см²).

Если l = 100 мм, F = 1000 Н (100 кгс), то Δl = 0,002 мм.

Кроме того, из-за отклонения от параллельности (поворота) боковичков от усилия сжатия погрешность еще увеличивается на Δl₁ = 0,001…0,003 мм. Тогда Δl_Σ = Δl + Δ l₁ = 0,002 + (0,001…0,003) = 0,003…0,005 мм.

Влияние смещения линии измерения в диаметральной плоскости круглого отверстия (результат измерения меньше действительного размера круглого отверстия; рис.17)

Чем больше d, тем меньше влияние смещения линии измерения на погрешность измерения.

 

с2 r R – r с1   с α R d     Рис.17 Схема смещения линии измерения

с – величина смещения линии измерения от диаметральной плоскости; R – радиус отверстия; r – радиус закругления губок (расстояние от центра радиуса r до точки контакта); (R – r) – расстояние от центра отверстия до центра радиуса закругления губки; d – диаметр отверстия

Влияние параллакса (рис.18)

 

«Параллакс» – от греческого «отклонение». Это явление наблюдается, когда плоскость шкалы и плоскость указателя не совпадают, а отметка шкалы и указатель рассматривают под некоторым углом к нормали к плоскости шкалы. Это явление характерно, например, для работы со штангенциркулем, микрометром, измерительной головкой. Для уменьшения влияния параллакса устанавливают определенные нормы толщины кромки линейки нониуса у штангенциркуля, кромки гильзы (барабана) микрометра (делают скосы), нормы расстояния от стрелки до плоскости шкалы у стрелочных приборов. Применяют также оптическое совмещение шкал (используя зеркала).

 

 

h – толщина нониуса плюс зазор между плоскостью планки нониуса и плоскостью штанги.

Δ = h _* tg α = h _* b / l

Обычно: l» 250 мм, b» 30 мм, h = 0…2 мм, Δ = 0,12 h.

Примем: h = 0,1 мм, α = 10°, тогда Δ = 0,1 _* tg10° = 17,6 мкм» 0,018 мм.

Если l = 250 мм, b = 30 мм, h = 0,1 мм (чаще бывает больше), то Δ = h _* b / l = 0,1 _* 30 / 250 = 0,012 мм; при h = 0,2 мм - Δ = 0,036 мм.

Для штангенинструментов при h = 0,3 мм и зазоре 0,1 мм - Δ = 0,048 мм.

нормаль

α₁ α₂

 

l

 

 

плоскость нониуса (стрелки)

h

90°

 

Δ_α2 Δ_α1 плоскость основной шкалы

плоскость нониуса

 

реальное расположение отметок

кажущееся расположение отметок

 

Рис.18 Схема влияние параллакса

 

 

 

Рекомендуемая литература

 

Основная литература

 

1. Закон РФ «Об обеспечении единства измерений» от 11 июня 2008 года.

2. Лифиц И.М. Стандартизация, метрология и сертификация. – М.: Изд-во «Юрайт», 2008.

3. Димов Ю.В. Метрология, стандартизация и сертификация. – Санкт-Петербург: Изд-во «Питер», 2010.

4.Никифоров А.Д. Метрология, стандартизация и сертификация. – М.: Изд-во Высш. шк.», 2010.

5.Сергеев А.Г., Терегеря В.В. Метрология, стандартизация и сертификация. – М.: Изд-во «Юрайт», 2010.

 

 

Дополнительная литература

 

1. РМГ-29-99. Метрология. Термины и определения.

2. ГОСТ 8.417-2002. Единицы величины.

3. ПР 50.2.006-98. Порядок проведения поверки средств измерений.

4. МИ 2277-94 ГСИ. Система сертификации средств измерений. Основные положения и порядок проведения работ.

5. ПР 50.2.002-94 ГСИ. Порядок осуществления государственного метрологического надзора за выпуском, состоянием и применением средств измерений аттестованными методиками выполнения измерений, эталонами и соблюдением метрологических правил и норм.

6. Ганевский Г.М., Гольдин И.И. Допуски, посадки и технические измерения в машиностроении: Учеб. для нач. проф. образования: Учеб. пособие для сред. проф. образования. – М.: ПрофОбрИздат, 2002. – 288 с.

7. Зайцев С.А., Грибанов Д.Д., Толстов А.Н., Меркулов Р.М. Контрольно-измерительные приборы и инструменты: Учебник для нач. проф. образования. – М.: Издательский центр «Академия», 2005. – 464 с.

8. Крылова Г.Д. Основы стандартизации, сертификации и метрологии: Учебник для вузов. –М.: Юнити, 2003. -671 с.

9. Тартаковский Д.Ф., Ястребов А.С. Метрология, стандартизация и технические средства измерений: Учебник для вузов. –М.: Высш. школа, 2002 (2001). -205 с.

10. Зайцев С.А., Грибанов Д.Д., Толстов А.Н., Меркулов Р.М. Контрольно-измерительные приборы и инструменты М.: Издательский центр «Академия», 2005. – 464 с.