Вероятность и закон нормального распределения вероятностей

 

Вероятность (Р) – действительное число в диапазоне от 0 до1, приписываемое случайному событию, представляющее отношение количества благоприятных случаев (n) ко всему количеству возможных случаев (N) в данной совокупности случаев, т.е. P = n / N. При n = 0, P = n / N = 0 / N = 0; при n = N, P = n / N = N / N = 1, т.е. событие становится неслучайным, а погрешность становится систематической.

При Р < 0,5 событие считают маловероятным, при Р ³ 0,5 событие считается вероятным. Чем больше N, тем больше вероятность и достоверность события. При N стремящемся к бесконечности, Р стремится к единице (закон больших чисел).

В теории вероятностей известны несколько законов распределения вероятностей. В большинстве случаев погрешности измерений подчиняются закону нормального распределения вероятностей – закону Гаусса (если говорить точнее, то имеет место нечто среднее между нормальным и равновероятностным законами).

Уравнение закона Гаусса, определяющее плотность вероятности Y при совпадении оси симметрии кривой с осью ординат:

где σ – теоретическая средняя квадратическая погрешность,

e» 2,7183 – основание натуральных логарифмов,

Δ – остаточная погрешность

Δ = x_i – m_х, где x_i – один из результатов,

m_х – средний арифметический результат или математическое ожидание случайной величины).

Одной из количественных характеристик случайных величин является дисперсия, которая характеризует рассеяние случайных величин относительно среднего арифметического значения (центра группирования случайных величин

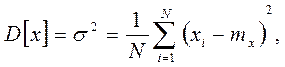– математического ожидания):

 

где N – общее количество случаев, x_i – отдельный результат, m_x – математическое ожидание.

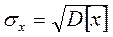Из формулы видно, что D[x] имеет квадратическое значение, что неудобно (например, получается мм²). Поэтому применяют более удобную величину – теоретическую среднюю квадратическую погрешность:

(здесь и далее, для обеспечения преемственности с курсом нормирования точности приняты те же обозначения; в метрологии σ_х = s).

Закон Гаусса действует при достаточно большом количестве равновлияющих и незначительных по величине случайных погрешностей.

Если учитывать только случайные погрешности в чистом виде, то закон Гаусса можно представить графически (рис.10) в виде теоретической кривой нормального распределения (кривой плотности распределения вероятностей)

y

34,136% 34,136%

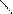_ Точки перегиба кривой

m_x = X = A_ср

Теоретическая кривая

 

13,592% 13,592%

 

2,137% 2,137%

0,135% 0,135%

x

-σ +σ

-2σ +2σ

±3σ = 6σ

 

Рис.10 Графическое изображение закона нормального распределения

y – плотность вероятности P, частность, в нашем случае частота появления i-той составляющей случайной погрешности; x_i – остаточная i-тая погрешность или погрешность отдельного i-того измерения, характеризующая отклонение случайной величины (результата измерения) от центра группирования (x_i = A_i – A_ср, где i = 1,2,…, n – порядковые номера измерений; A_i – результат i-того измерения; A_ср – средний арифметический результат измерений, соответствующий центру группирования результатов (стремится к математическому ожиданию)).

Теоретическая средняя квадратическая погрешность характеризует зону рассеяния – разброса случайных величин относительно центра группирования:

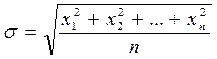
(в знаменателе n, если n ³ 25; n –1, если n < 25).

Средняя вероятная погрешность γ = 0,675 _* σ» 0,7 σ.

Кривая Гаусса обладает свойством, что если площадь, заключенную между кривой и осью абсцисс принять за 100% (или равной 1), то площадь, заключенная между частью кривой и отрезком в пределах ± σ на оси абсцисс составит»68%, а между частью кривой и отрезком в пределах ± 2σ составит»95,456% от всей площади (т.е. доверительная вероятность 95,456% или 0,95456» 0,95). Распределение этих площадей соответствует распределению случайных погрешностей.

При измерениях практически принимают Δlim_и = ± σ _и, которую называют предельной (наибольшей допустимой) случайной погрешностью измерения, а зону рассеяния погрешностей в пределах ± 2σ _и называют полем рассеяния погрешностей измерений.

Так как вся площадь составляет 100% (или равна 1), а площадь, соответствующая вероятности предельной случайной погрешности измерения 95,456%, то оставшаяся часть площади равна 4,544% (риск выхода погрешности за пределы ± 2σ _и). Следовательно, с вероятностью очень близкой к 100% (или 1) можно утверждать, что случайные погрешности измерений, при достаточно большом количестве измерений (или составляющих случайной погрешности), не будут выходить за пределы ± 2σ _и, т.е. будут считаться допустимыми. Но, так как возможен выход погрешности, как в плюс, так и в минус, то риск составляет 2,272%» 2,3%. Погрешности измерений, превышающие ± 2σ _n, относят к грубым.

При изготовлении (обработке) изделий, в том числе деталей СИ, величину Δ_тlim = ± 3σ _т называют предельной случайной погрешностью изготовления (технологической). Детали, имеющие погрешности за пределами ± 3σ _т, представляют собой брак.

Анализ кривой Гаусса показывает, что:

- малые по величине погрешности встречаются значительно чаще, чем большие;

- одинаковые по абсолютной величине погрешности, но противоположные по знаку, встречаются одинаково часто;

- большинство результатов измерений группируются около середины поля рассеяния (т.е. имеют значения погрешностей близкие к нулю, но не равные ему);

- с увеличением количества измерений среднее арифметическое из случайных погрешностей данного ряда стремится к нулю (благодаря чему, увеличивая количество измерений одной величины можно уменьшать влияние случайных погрешностей на результаты измерений, практически исключая их);

- наиболее достоверные результаты при многократных измерениях представляют собой средние арифметические из получаемых результатов (и наоборот);

- погрешности, выходящие за пределы ± 2σ _и, признаются грубыми и исключаются из результатов измерений.

Для оценки степени уменьшения влияния случайной погрешности пользуются правилом 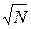, где N – количество измерений. Из этого правила следует, что если одну и ту же величину измерять 4 раза, то влияние случайной погрешности на результаты измерений уменьшатся в 2 раза (если принять за результат А_ср), если измерить 9 раз, то уменьшится в 3 раза и т.д.