В настоящее время для обработки экспериментальных данных прямых многократных измерений принято использовать методы математической статистики. При этом следует помнить, что применение этих методов позволяет получить корректные результаты только в том случае, когда из экспериментальных данных исключены систематические погрешности.
Обработка экспериментальных данных прямых многократных измерений в общем случае предусматривает выявление закономерности поведения случайной погрешности (определения закона распределения) и статистические процедуры исключения грубых погрешностей.
Нормальный закон распределения является наиболее распространенным законом распределения случайных величин, в том числе и случайных погрешностей. Поэтому в практике обработки экспериментальных данных, когда число измерений мало (не превышает 5…25), пользуются вполне оправданным предположением, что закон распределения случайной погрешности является нормальным, а грубые погрешности не выявляются или определяются и отбрасываются интуитивно.
Методы математической статистики предполагают определение вместо характеристик нормального распределения их оценок. Так, вместо математического ожидания М[Х], т.е. значения величины, вокруг которого группируются результаты отдельных измерений при бесконечном числе измерений, определяют его оценку, которая представляет собой среднее арифметическое `Х при конечном числе измерений: 
М[Х] ≈ `Х = 
 i,
i,
где Xi – результат i –го измерения, n – число измерений.
Вместо среднеквадратического отклонения σ, характеризующего рассеяние результатов отдельных измерений относительно математического ожидания, определяют оценку среднеквадратического отклонения результата измерений по формуле
S(`Х)= 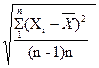 .
.
Также при обработке экспериментальных данных прямых многократных измерений принято вычислять интервальную оценку погрешности, которая оп-
ределяется с использованием точечной погрешности S(`Х) и доверительных интервалов.
Для обеспечения единства технических измерений задаются значением доверительной вероятности Рд = 0,95 и определяют значение доверительного интервала. Коэффициент t обычно определяют по таблице вместо того чтобы рассчитывать по сложной формуле, описывающей распределение Стьюдента.
Последовательность обработки экспериментальных данных прямых многократных измерений приведена ниже. При этом предполагается:
результаты измерений являются исправленными, т.е. из них исключена известная систематическая погрешность;
неисключенные систематические погрешности настолько малы, что ими можно пренебречь;
результаты измерений являются равнорассеянными величинами (такие результаты получаются при выполнении измерений одним оператором с помощью одних и тех же средств измерений);
из результатов измерений исключены грубые погрешности (промахи);
число измерений не превосходит 15…25 (в этом случае признается и не проверяется нормальность распределения случайных погрешностей).
Алгоритм обработки экспериментальных данных прямых многократных измерений:
1. Получение n результатов наблюдений.
2. Вычисление среднего арифметического`Х.
3. Вычисление оценки среднеквадратического отклонения результата измерения S(`Х).
4. Принятие значения доверительной вероятности Рд (для технических измерений Рд = 0,95).
5. Определение коэффициента t в зависимости от Рд и n по таблице распределения Стьюдента.
6. Определение доверительных границ Δд случайной погрешности.
7. Запись результата измерений с использованием правил округления в виде А =`Х ± Δд с обязательным указанием (Рд =; n =).
Обработка экспериментальных данных прямых однократных измерений.
Результаты однократных измерений также являются случайными величины, но из-за незнания закона распределения не могут быть подвергнуты статистической обработке. Поэтому результат прямого однократного измерения записывают в виде интервальной оценки:
Α = X ± Δ,
где X – значение физической величины, найденное по шкале измерительного средства; Δ – абсолютная погрешность для найденного значения X, определяемая по технической документации на средство измерения.
Для избежания получения промахов при однократных измерениях допускается проведение 2 - 3 замеров с нахождением среднего арифметического результата измерения, но без последующей статистической обработки.






