Эта модель связевая. Первичное звено рассматривается как канал связи. На выходе его формируется М-мерные наборы 
. ВО восстановительный орган или схема декодирования, который на основании правила принимая решения формирует либо 0 или 1. На вход подается либо 0 либо 1.
Отказ - связанное с изменением 
значений.
КС – канал связи.
реакция на конкретный набор(формирование 0 и 1 по определенному правилу).
вероятность ошибочного срабатывания
вероятность безошибочного срабатывания
Передаточная матрица, она стохастическая, это значит, что: 
– условие нормирования.
– безошибочно формирует 0, безотказное срабатывание
- вместо правильного нуля формируется логичная 1
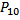- вместо правильной единицы формируется логичный ноль
- условно правильная единица.
Для получения детального анализа необходимо знать статистические свойства сигнала.
- априорная «безусловная» вероятность формирования 0 или 1 на выходе системы.
Правила декодирования оказывают существенное влияние на достоверность передачи.
ВО – декодер в КС.
Таким образом, стоит задача выбора правила декодирования – оптимального (наименьшая вероятность отказа системы).
Определение оптимального правила восстановления
| 
| 
| 
|
Выбор оптимального правила: установить соответствие между набором на входе и значением на выходе.
, где
– безусловная вероятность формирования 000, априорная вероятность того, что на выходе «0», если на входе «000».
- условная вероятность того, что истинной будет «0» значение.
Необходим критерий выбора, т.е. необходима некая альтернатива:
, где «1» - истина, при условии, что на выходе КС «000».
Если имеет место [000] набор, то делаем предположение, что 0 – истинна, оценив апостериорную вероятность формируем [000], если 1 на выходе.
И ставим то значение, у которого апостериорная вероятность больше.
Такая процедура повторяется для каждого набора.
P(0) задано. Это статистическое свойство сигнала может быть задано по «плотности» нулевых и единичных значений выполняемых резервными звеньями функций.
Правило максимума апостериорной вероятности.
Если выполняется функция коньюнкции, по вероятность P(1)=1/8
2 путь -> проведение статистического эксперимента. Как определить условную вероятность появления наборов, при истинном 0 или 1.
Возьмем за базу [111]: 
- вероятность формирования 0. если 0 истинно.
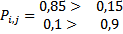
Апостериорная вероятность: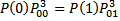 
Особенности подхода:
1. Часто оптимальная функция может быть отлична от мажоритарной.
2. свойство усиливается при ассиметричном распределении входных сигналов и ассиметричной матрице.
3. если статистика одинакова - матрицы симметричны полностью, то оптимальная функция является мажоритарной функцией.
4. вероятность формируется путем суммирования апостериорной вероятности 0 и 1.
– подмножество наборов, в которых, исходя из выбранного правила восстановления поставлено i значение.
P – элемент статистической матрицы (симметричной). 
зависит от P.
1. пусть элементы статистической матрицы изменяются (уменьшаются).
2. ….
