Под показателем надежности понимается количественная характеристика одного или нескольких свойств, составляющих надёжность объекта. Различают единичный, комплексный и нормативный показатели надежности. Единичный и комплексный показатели надежности относятся соответственно к одному и нескольким свойствам, составляющим надежность объекта. Нормативный показатель надежности устанавливается нормативно-технической документацией.
Из всего многообразия показателей надежности рассмотрим лишь несколько наиболее важных и характерных.
Вероятность безотказной работы - вероятность того, что в пределах заданной наработки отказ объекта не возникает.
Интенсивность отказов - предел отношения условной вероятности отказа на интервале наработки после данного момента при условии, что до данного момента отказ не возник, к продолжительности этого интервала при его уменьшении до 0.
Наработка - продолжительность или объем работы, выполненный объектом.
Параметр потока отказов – предел отношения вероятности отказа на интервале времени или наработки после данного момента к продолжительности этого интервала при его уменьшении до 0.
Наработка на отказ – отношение наработки восстанавливаемого объекта к математическому ожиданию числа его отказов в течении этой наработки.
Наработка до отказа – математическое ожидание наработки объекта до первого отказа.
Среднее время восстановления – математическое ожидание времени восстановления работоспособности объекта.
Коэффициент готовности – вероятность того, что объект окажется работоспособным в любой момент времени кроме периодов, в течение которых использование объекта по назначению не предусматривается.
Коэффициент технического использования – вероятность того, что объект, находясь в режиме ожидания, окажется работоспособным в произвольный момент времени и с этого момента будет работать безотказно в течение заданного времени.
Практически все элементы систем электроснабжения относятся к ремонтируемым изделиям, т.е. являются восстанавливаемыми объектами.
Восстанавливаемый объект – объект, работоспособность которого в случае возникновения отказа подлежит восстановлению в рассматриваемой ситуации. Работоспособность невосстанавливаемого объекта не подлежит и не восстанавливается в случае возникновения отказа.
Процесс эксплуатации восстанавливаемых объектов можно представить как последовательность прямоугольных импульсов, соответствующих интервалам простоя (ti), чередующихся с интервалом работоспособности (Qi). Математической моделью процесса эксплуатации электрооборудования может являться следующий случайный процесс (рис.I.2.I.).
Рис.I.2.I. Случайный процесс, соответствующий состояниям работоспособности и отказа электрооборудования.
Этот процесс является случайным, т.к. отрезки времени ti и Qi носят случайный характер.
Вероятность безотказной работы объекта в течение заданного времени работы t0, начиная с момента окончания (К-I)- го восстановления-это вероятность того, что объект проработает безотказно в течение некоторого интервала времени при условии, что начало интервала совпадает с моментом окончания (К-1) восстановления объекта.
Рк (to)= Р {Q k ≥ to } = 1- FK (to), (1.1)
где Fk (to)- функция распределения случайной величины Qk.
Статистически вероятность безотказной работы [Рk (tо)] представляет собой отношение числа объектов, у которых время работы от момента окончания (К-I)- го восстановления до момента наступления К- го отказа больше заданного времени работы tо, к общему числу объектов.
Nk (to) nk (tо)
Рк (tо)= ——— = 1- ———,
Nk (0) Nk (0) (I.2)
где Nk (to)- число не отказавших ни разу к моменту t'= to;
Nk (0)- число исправных объектов в момент t'= 0;
nk (to)- число объектов, отказавших хотя бы один раз к моменту t'= to.
Вероятность отказа объекта в течение заданного времени работы to, начиная с момента окончания (К-I)- го восстановления- это событие, противоположное вероятности безотказной работы и представляет собой вероятность того, что объект откажет в течение заданного интервала времени to при условии, что начало этого интервала совпадает с момента окончания (К-I)- го восстановления объекта.
Qk (to) = Р {Q k < to } = FK (to) = 1-Рк (to) (I.3)
Эта вероятность может быть определена как отношение числа объектов, у которых время работы от момента окончания (К-I)- го восстановления до момента наступления К - го отказа меньше заданного времени работы to, к общему числу объектов.
nk (to) Nk (to)
Qk (to) = ——— = 1 - ———
Nk (0) Nk (0) (I.4)
Графическое изображение понятий Рк (to) и Qk (to) приведено на рис. I.2.2.
13 
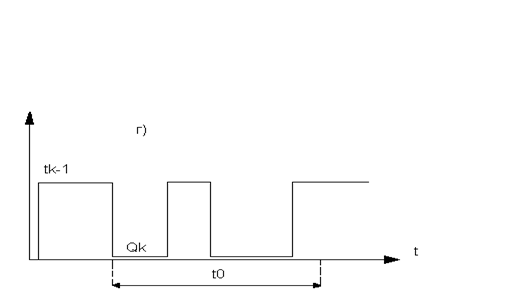
Рис.I.2.2. Диаграммы, поясняющие понятия Рк (to) и Qк (to):
а) – безотказная работа элемента;
б), в), г) – случаи отказов элемента.
Последовательность событий, происходящих одно за другим в различные моменты времени t, представляют собой поток событий. В данном случае мы имеем поток отказов, причем это поток однородных событий, отличающихся только моментами их наступления.
Важной характеристикой потока отказов объекта является интенсивность отказов в момент времени t.
1 d f (t)
λ(t) = ——— —— F (t) = ——
1- F (t) dt P (t) (I.5)
Она представляет собой плотность вероятности отказа объекта к моменту времени t при условии, что до этого момента отказ изделия не произошел.
Статистически λ(t) – есть отношение числа отказов в интервале времени [t, t+ ∆t] к произведению числа исправных объектов в момент времени t на длительность интервала времени ∆t.
n(t+∆t) – n(t) ∆n (t, ∆t)
λ(t)= —————— = —————,
N(t) ∆t N (t) ∆t (I.6)
где n(t) – число объектов, отказавших к моменту времени t;
N(t) – число объектов, исправных к моменту времени t;
∆n(t, ∆t) – число объектов, отказавших именно в интервале времени
[t, t + ∆t].
Другой, не менее важной характеристикой потока является параметр потока отказов, представляющий собой среднее количество отказов восстанавливаемых элементов в единицу времени,
Q(t, t + ∆t) d Q
ω= lim ————— = ———,
∆t→0 ∆t d t (I.7)
где Q (t, t + ∆t) – вероятность того, что объект откажет в интервале времени или наработки от t до t + ∆t.
Поток отказов электрооборудования можно считать стационарным, т.к. вероятность отказов за фиксированный промежуток времени зависит только от длины промежутка и не зависит от положения промежутка на оси времени, т.е. плотность потока отказов постоянна во времени.
Поток отказов характеризуется отсутствием последствий, поскольку для любых неперекрывающихся участков времени число отказов, приходящихся на один из них, не зависит от числа отказов, происходящих в другие интервалы времени.
Кроме того, поток отказов является ординарным, т.к. вероятность двух и более отказов на отрезке времени ∆t несравнимо мала с вероятностью появления одного отказа.
Для ординарных потоков справедливо равенство
∆n (t, ∆t)
ω(t)= λ(t)= —————
N (t) ∆t (I.8)
Стационарный поток характеризуется постоянством значений ω(t) и λ(t), т.е. ω(t)= ω= const и λ(t)= λ= const
ω и λ= const (I.9)
Если ординарный поток к тому же еще и стационарный, то
ω = λ= const (I.I0)
Если поток обладает всеми тремя свойствами, т.е. является стационарным, ординарным и характеризуется отсутствием последействия, то он называется простейшим пуассоновским потоком, а вероятность наступления n событий за время t определяется по формуле Пуассона. Для такого потока математическое ожидание числа событий за время t
М (х)= ωt (I.11)
и закон Пуассона принимает вид
k k
(ωt) (λt)
Pk (t)= ——— exp (-ωt)= ——— exp (-λt) (I.I2)
K! K!
Поток отказов электрооборудования, как правило, является нестационарным, что обуславливается наличием периода приработки и явления старения изоляции, износом и разрегулировкой отдельных частей, а также влиянием метеорологических факторов. Реальная кривая изменения параметра потока отказов электрооборудования от времени эксплуатации представлена на рис. I.2.3.
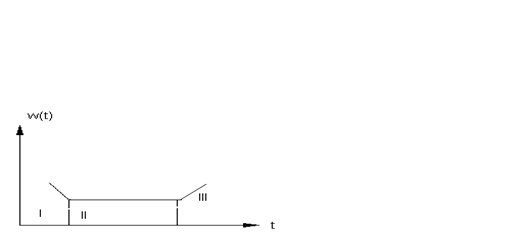
Рис. I.2.3. Кривая изменения ω (t) электрооборудования от времени эксплуатации.
I- участок, соответствующий периоду приработки.
На этом отрезке времени выявляются дефекты изготовления и монтажа оборудования;
II- участок, соответствующий периоду нормальной эксплуатации. Значение ω, соответствующее этому периоду, принимается для оценки надежности;
III- участок, обусловленный износом и старением.
В период нормальной эксплуатации повреждаемость стабильна, поэтому для участка II имеет место равенство
ω(t)= ω= const и λ(t)= λ= const
Если учесть ординарность потока отказов, то
ω = λ= const
Это и есть те условия, которые позволяют считать поток отказов электрооборудования простейшим пуассоновским потоком.
Вероятность отсутствия отказов за время t, т.е. вероятность безотказной работы Pk (t) определится из (I.I2) при условии к=0
Р0 (t)= exp (-ωt)= exp (-λt) (I.I3)
Тогда вероятность отказа будет определяться как
Q0 (t)= 1- Р0 (t)= 1- exp (-ωt)= 1- exp (-λt) (I.I4)
Графическое представление зависимостей, соответствующих (I.I3) и (I.I4) приведено на рис. I.2.4.
Рис. I.2.4. Кривые вероятности безотказной работы Р(t) и вероятности отказа Q(t).
Эти кривые представляют собой экспоненты с параметром
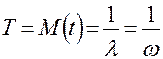(I.I5)
Поскольку 
n (t, t) в выражении (I.8) есть величина случайная, то при определении ω необходимо найти доверительные границы, в пределах которых находится действительная величина ω. Эти границы определяются с некоторой вероятностью, называемой доверительной вероятностью или коэффициентом доверия.
Границы доверительного интервала вычисляются по формулам
- нижняя:
ω
ωk= —— 
r1
ω
- верхняя: ωk= ——
r2
где r1 и r2 определяются по таблице I приложения при соответствующей доверительной вероятности α.
Опыт показывает, что при оценке параметра потока отказов электрооборудования достаточной является доверительная вероятность 0,91-0,95.
Параметр потока отказов имеет тенденцию снижения вследствие повышения качества изделий и повышения культуры эксплуатации. Поэтому для оценки надежности на перспективный период необходимо определить параметр потока отказов для ряда предшествующих лет, построить график ω= f (t) и экстраполировать его на требуемую перспективу. Полученный таким образом параметр потока отказов достаточно точен, если уровень перспективы не превышает 10 лет.
Мы уже говорили о том, что отказы электрооборудования и время работы между отказами есть случайные величины, а математическое ожидание времени работы между отказами называется наработкой на отказ. Эта величина определяется как среднее значение времени между отказами
(I.I6)
где ti- время работы оборудования между двумя отказами;
n- число отказов.
После периода приработки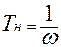 
Принимая за единицу времени 1 год, получаем значение наработки на отказ в часах
(I.I7)
где 8760- число часов в году.
Наработка до отказа представляет собой среднее арифметическое реализаций времени работы объекта до отказа
(I.I8)
где 
- начальное число объектов
- реализация времени работы до отказа для i- го объекта (в порядке поступления отказов).
Среднее восстановление τ- среднее арифметическое реализаций времени восстановления объектов или среднее арифметическое реализаций времени восстановления одного и того же объекта.
(I.I9)
где ti- время, затрачиваемое на отыскание и устранение каждой неисправности;
п- число отказов.
Данная величина (τ) существенно зависит от опыта обслуживающего персонала, оснащенности его соответствующими средствами и определяется на основе опыта эксплуатации.
Коэффициент готовности- это отношение суммарного времени исправной работы элемента к общему времени исправной работы и времени восстановления, взятых за один и тот же период эксплуатации.
(I.20)
Статистически эта величина определяется как отношение числа объектов, находящихся в состоянии работоспособности в произвольный «удаленный» момент времени, к общему числу объектов
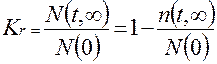(I.21)
где 
- число объектов, находящихся в состоянии работоспособности в произвольный «удаленный» момент времени;
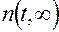- число объектов, находящихся в состоянии отказа в «удаленный» момент времени;
- общее число объектов.
Понятие, противоположное Кr, есть коэффициент вынужденного простоя- это вероятность того, что элемент будет неисправен в промежутке между плановыми ремонтами
(I.22)
Учитывая (1.17), получаем
(1.23)
Поскольку 
, то
(1.24)
Если в течение некоторого промежутка времени суммарная наработка составляет Траб, а простои на ремонт и обслуживание составляют соответственно Тав и Тпл.р и учитывая при этом оборудование, выведенное в резерв (Трез), коэффициент технического использования определяется по выражению
т.и.= 
(1.25)
Так как длительность нахождения оборудования в резерве невелика, то выражение (1.24) принимает вид
т.и.= 
(1.26)
Так как рассматривая отдельные элементы или же всю систему в целом мы в первую очередь выясняем вопрос- работают они или не работают, исправны или неисправны, то, очевидно, и вероятность безотказной работы Рк (to) и вероятность отказов Qk (to) связаны между собой соотношением
(1.27)
Для большинства элементов систем электроснабжения вероятность появления того или иного числа отказов в заданный промежуток времени подчиняется закону Пуассона
(1.28)
где m- число отказов
t- период времени
ω- параметр потока отказов.
Если рассматривать какой-либо отдельный элемент и принять длительность периода, равной одному году, то вероятность безотказной работы данного элемента составит
(1.29)
Однако следует иметь в виду, что закон Пуассона применим в случае рассмотрения внезапных отказов случайного характера. Отказы, связанные с износом, как правило, не следуют этому закону.
2. Показатели плановых ремонтов
Современные системы электроснабжения представляют собой сложнозамкнутые, со множеством основных и резервных элементов системы, надежность которых определяется как показателями надежности элементов, так и показателями их плановых ремонтов. Наиболее тяжелые последствия для системы электроснабжения будут иметь место при отказах элементов в период ремонта.
Показателями плановых ремонтов являются частота плановых ремонтов ωn (1/год) и средняя продолжительность планового ремонта Тn (ч.).
По аналогии с наработкой на отказ и коэффициент вынужденного простоя определяется продолжительность межремонтного периода
(2.1)
и коэффициент ремонтного режима
(2.2)
Количественные значения показателей плановых ремонтов как и показателей надежности могут быть определены на основе систематических данных, полученных в процессе эксплуатации электрооборудования за достаточно продолжительный срок. Такие данные, отвечающие среднестатистическим показателям отечественных энергосистем, получены проф. П.Г.Грудинским и приведены в таблице 2 Приложения.
Контрольные вопросы:
1. Пояснить различие между понятиями «параметр потока отказов» и «интенсивность отказов».
2. Допущения, позволяющие считать поток отказов простейшим Пуассоновским потоком. Пояснить их.
3. Привести выражения вероятности безотказной работы и вероятности отказа.
4. Коэффициент готовности, коэффициент вынужденного простоя, коэффициент технического использования. Выражения для их определения.
5. Наработка на отказ, наработка до отказа.
6. Показатели плановых ремонтов.
