Статистическая обработка информации об отказах объектов осуществляется в следующем порядке:
1) составление сводки исходных данных;
2) проверка качества исходных данных;
3) построение эмпирического распределения и выбор закона распределения отказов;
4) расчет показателей надежности.
Сводку исходных данных (выборку) по определенному виду объектов составляют в виде таблицы (табл.4.1), в которой указывают наименование объекта, значения наработок до отказа элементов, приведших к отказу объекта в рассматриваемый промежуток времени.
к- количество интервалов
Значение интервала находят по формуле:
,
где tк, tо – максимальное и минимальное значения времени наблюдения.
Число отказов mi, приходящихся на каждый i -тый интервал, отнесенное к общему числу отказов m, определяет частоту отказов
.
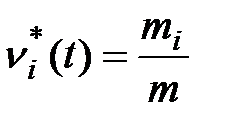Полученные значения 
сводятся в табл.4.2. Сумма частот отказов всех интервалов, должна быть равна единице.
Проверка исходных данных заключается в оценивании достоверности и отсеивании недостоверной информации. Члены выборки (суммы отказов по интервалам) группируют в виде возрастающей последовательности, называемой вариационным рядом. Вначале проверяют крайние члены выборки. Возможен случай, когда крайние члены этой последовательности резко отличаются по величине от остальных.
Сводка исходных данных Таблица 4.1
| Объекты | Номер элемента | Наработка до отказа, ч |
| 1-й объект | ||
| ... | ||
| j- й объект | ||
| ... | ||
| N-й объект |
Таблица 4.2 Частоты отказов
| Интервал, ч | 
|
| Частота отказов |   
|
В этом случае следует произвести тщательный количественный анализ с целью установления, не является ли такое отличие следствием наличия в исходных данных ошибочных или недостоверных сведений.
14. Выбор закона распределения наработок при расчете количественных
показателей надежности
Для определения вида закона распределения по статистическим данным строят гистограмму. Гистограмма – график статистической плотности распределения случайной величины в виде ступенчатого многоугольника.
Проверку допустимости принятого теоретического закона (согласованность экспериментальной и теоретической кривых) проводят по различным критериям согласия, из которых наиболее распространенными являются критерий Колмогорова и критерий 
(хи-квадрат) Пирсона. Первый используется в случае, когда параметры распределения известны до опыта и требуется после опыта лишь проверить согласованность теоретического и экспериментального распределений, второй – при неизвестных параметрах распределения случайной величины.
Алгоритм применения критерия при оценивании согласия теоретического и статистического распределений с учетом известных значений статистических частот 
предполагает:
Определение меры расхождения
,
где 
– теоретическая частота; – статистическая частота случайной величины в i -м интервале; к – число интервалов; m – объем выборки.
Нахождение числа степеней свободы
r = к - (s + 1),
где s – число параметров теоретического распределения.
Нахождение теоретического значения критерии определяется доверительной вероятностью 
= (0,9; 0,95; 0,99; 0,999) и числом степеней свободы r которая определяется по формуле
k- количество интервалов наблюдения
s-число параметров теоретического распределения
T0-* математическое ожидание
σ*-дисперсия
| Рис.4.2. Примерный вид распределения функции f(t) 1 – гистограмма; 2 – полигон; 3 – аппроксимирующая функция f(t) (ф-я норм.Закона распредел.) |
Для определения теоретической величины ν i необходимо воспользоваться формулой Лапласа
tверхн.i- верхняя граница интервала Δt i
Сравнение теоретического и статического критерия : 
> 
то в этом случае гипотезу о принадлежности исходной выборки закону распределения принимают. В противном случае не принимают.
