Количественные показатели надежности восстанавливаемыхэлементовЭУ

Безотказность, долговечность, ремонтопригодность и сохраняемость восстанавливаемых элементов ЭУ имеют количественные показатели.

К показателям безотказности относятся: параметр потока отказов, вероятность безотказной работы, наработка на отказ.

Эксплуатация многих восстанавливаемых ЭУ может быть описана следующим образом: в начальный момент времени ЭУ начинает работу и функционирует до отказа. При отказе происходит восстановление, и ЭУ работает до следующего отказа и т.д. Оказалось удобным рассматривать процесс возникновения отказов как поток случайных событий. Последовательность отказов, происходящих один за другим в случайный момент времени, носит название потока отказов.

Параметр потока отказов – плотность вероятности возникновения отказа восстанавливаемой ЭУ, определяемого для рассматриваемого момента времени.

Статистический параметр потока отказов определяется: 1/ч,

где – колличество отказов в интервале времени 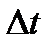; N –общее количество восстан. элементов ЭУ.

Потоки отказов по своему характеру бывают самыми различными. Наибольшее практическое и теоретическое применение находит простейший поток, который характеризуется тремя свойствами:

– ординарности, выражающейся в том, что вероятность появления двух или более отказов ЭУ в течение промежутка времени стремится к нулю при уменьшении этого промежутка, т.е.

– стационарности, заключающейся в том, что параметр потока отказов является постоянным, т.е. =const;

– отсутствия последействия, состоящем в том, что отказы, происшедшие ранее, не влияют на возникновение последующих отказов.

Из перечисленных свойств следует, что при простейшем потоке отказов ,

т.е. параметр потока отказов совпадает с интенсивностью отказов ЭУ.

Вероятность безотказной работы определяется:

.

Приведенный на рис.2.7 график поясняет изменение вероятности безотказной работы Р во времени t.

 

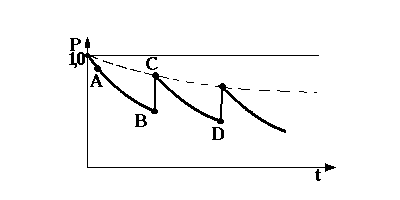
2.7. График изменения P(t)

При отправке элементов ЭУ с завода-изготовителя значение Р(t) близко к 1 (точка А). За время транспортировки ЭУ и ее хранения на базах вероятность Р(t) снижается вследствие старения элементов, воздействия внешних климатических условий и ряда других факторов (точка В). После поступления элементов ЭУ на монтаж необходимо контролировать их состояние, чтобы предотвратить возможность установки неработоспособного электрооборудования.

В результате устранения обнаруженных дефектов значение Р повышается почти до такого уровня, на котором она была до транспортировки и хранения (точка С

Из рассмотрения графика следует, что проверка с устранением обнаруженных дефектов – эффективное средство поддержания надежности и повышения эффективности ЭУ.

Наработка на отказ – отношение наработки восстанавливаемой ЭУ к математическому ожиданию числа ее отказов в течение этой наработки. Другими словами, это математическое ожидание времени между двумя ближайшими последовательными отказами. В общем случае наработка на отказ зависит от длительности периода, в течение которого она определяется. Это обусловлено непостоянством характеристики потока отказов. Для периода нормальной работы при экспоненциальном законе распределения отказов справедливо .

Статистически она определяется ,

где – время безотказной работы между (i-1) и i отказами;

m – общее число отказов.

В качестве основных показателей долговечности используют средний ресурс и средний срок службы.

Средний ресурс – математическое ожидание ресурса с учетом восстановления. Для элементов ЭУ переход в предельное состояние определяется наступлением момента, когда их дальнейшая эксплуатация и применение невозможны или нецелесообразны по одной из следующих причин: 1. из-за невозможности поддержания безопасности, безотказности или эффективности применения элементов ЭУ на допустимом уровне;2. в результате старения элементов ЭУ, когда на ремонт требуются недопустимо большие затраты, или он не обеспечивает необходимой степени восстановления работоспособности.

Статистически ресурс оценивается зависимостью: ,

где N – число электроустановок; – ресурс i -й электроустановки.

Средний срок службы – математическое ожидание срока службы (календарной продолжительности эксплуатации) ЭУ от начала эксплуатации до наступления предельного состояния с учетом восстановления. Статистически его можно определить

,где – срок службы i -й электроустановки.

Ремонтопригодность характеризуется показателями: вероятностью восстановления в заданное время t_в и средним временем восстановления Т_в.

В качестве количественной меры ремонтопригодности применяется вероятность того, что ЭУ будет отремонтирована (или приведена в состояние, пригодное для использования) за время t .

Для практических расчетов наиболее часто применяется экспоненциальный закон распределения времени ремонта, для которого справедливо соотношение ,

где – интенсивность ремонта ЭУ.

Обычно в качестве основного показателя ремонтопригодности используется среднее время восстановления ЭУ Т_в, которое складывается из трех составляющих:

среднего времени контроля Т_к;

среднего времени поиска дефекта Т_п;

среднего времени устранения дефекта Т_у.

На практике Т_п>Т_у.

Статистически среднее время восстановления определяется

,

где t_i – время, затраченное на восстановление i -го отказа; m - количество отказов.

В качестве показателей сохраняемости используют средний срок сохраняемости, который определяется по формуле:

,

где – параметр потока отказов восстанавливаемых элементов ЭУ при хранении.