Для анализа и синтеза схем в ЭВМ при алгоритмизации и программировании решения задач широко используется математический аппарат алгебры логики.
Алгебра логики – это раздел математической логики, значения всех элементов (функций и аргументов) которой определены в двухэлементном множестве: 0 и 1. Алгебра логики оперирует с логическими высказываниями.
Высказывание – это любое предложение, в отношении которого имеет смысл утверждение о его истинности или ложности. При этом считается, что высказывание удовлетворяет закону исключенного третьего, т.е. каждое высказывание или истинно, или ложно и не может быть одновременно и истинным, и ложным.
Пример 4.11. Высказывания: "Сейчас идет снег" – это утверждение может быть истинным или ложным; "Вашингтон – столица США" – истинное утверждение; "Частное от деления 10 на 2 равно 3" – ложное утверждение.
В алгебре логики все высказывания обозначают буквами а, b, с и т.д. Содержание высказываний учитывается только при введении их буквенных обозначений, и в дальнейшем над ними можно производить любые действия, предусмотренные данной алгеброй. Причем если над исходными элементами алгебры выполнены некоторые разрешенные в алгебре логики операции, то результаты операций также будут элементами этой алгебры.
Простейшими операциями в алгебре логики являются операции логического сложения (иначе, операция ИЛИ, операция дизъюнкции) и логического умножения (иначе, операция И, операция конъюнкции). Для обозначения операции логического сложения используют символы + или V, а логического умножения – символы * или ö.
Правила выполнения операций в алгебре логики определяются рядом аксиом, теорем и следствий.
В частности, для алгебры логики выполняются законы:
1) сочетательный:

2) переместительный:

3) распределительный:

Справедливы соотношения:

Наименьшим элементом алгебры логики является 0, наибольшим элементом – 1. В алгебре логики также вводится еще одна операция – операция отрицания (иначе, операция НЕ, операция инверсии), обозначаемая чертой над элементом.
По определению: 
Справедливы, например, такие соотношения: 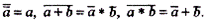
Функция в алгебре логики – это алгебраическое выражение, содержащее элементы алгебры логики а, b, с..., связанные между собой операциями, определенными в этой алгебре.
Пример 4.12. Примеры логических функций:
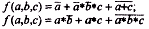
Согласно теоремам разложения функций на конституэнты (составляющие) любая функция может быть разложена на конституэнты "1":

и т.д.
Эти соотношения используются для синтеза логических функций и вычислительных схем.






