Математический аппарат теории вероятностей широко используется в метрологии. Рассмотрим некоторые свойства законов распределения вероятности, являющихся моделями эмпирических законов распределения, получаемых из экспериментальных данных методами математической статистики.
Функция распределения вероятности F (x) и плотность распределения вероятности P (x) служат в теории вероятности моделями эмпирических законов распределения экспериментальных данных.
Свойства законов распределения вероятности:
1. Функция F (x) определяет вероятность того, что отдельный результат, полученный по формулам (1, 4) будет меньше ее аргумента.
2. Так как вероятность не может быть отрицательной, то F (x) ³ 0 всегда; и чем больше х, тем больше вероятность того, что ни один результат, полученный по формулам, не превысит этого значения, так как F (x) – функция неубывающая.
3. Результат, полученный по приведенным выше формулам, больше некоторого х 1 с вероятностью F (x 1) и меньше х 2 с вероятностью F (x 2):
 .
.
4. P (x i) связано с F (x i) формулой:
 ,
,
то есть P (x) является дифференциальной функцией распределения вероятности.
5. Так как F (x) – функция неубывающая, то ее производная неотрицательна.
6. Вероятность того, что отдельный результат, полученный по формулам, окажется в заданном интервале, равна площади, ограниченной графиком функции P(x), осью абсцисс и перпендикулярами на концах интервала:

7. При расширении интервала до бесконечности рассматриваемое событие становится достоверным. Поэтому площадь, ограниченная графиком функции P (х) и осью абсцисс, равна 1:
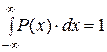 .
.
Описание отсчета или результата измерения с помощью законов распределения вероятности является наиболее полным, но неудобным. Во многих случаях ограничиваются приближенным описанием закона распределения вероятности с помощью его числовых характеристик,или моментов. Все они представляют собой некоторые средние значения, причем, если усредняются величины, отсчитываемые от начала координат, моменты называются начальными, а если от центра закона распределения – центральными.
Общее правило написания моментов:
 ,
,
где r – номер момента.
Важнейшим начальным моментом является первый, его называют математическим ожиданием M (x) или средним значением результатов:
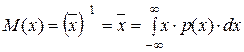 .
.
Свойства математического ожидания:
1) математическое ожидание неслучайного числа равно самому этому числу:
M (a) = a, где а – неслучайное число, а = const;
2) постоянный множитель можно выносить за знак математического ожидания:
M (a · x) = a · M (x);
3) математическое ожидание алгебраической суммы случайных чисел равно алгебраической сумме их математических ожиданий:
M (x + y - z) = M (x)+ M (y) – M (z);
4) математическое ожидание произведения независимых случайных чисел равно произведению их математических ожиданий:
M (x · y) = M (x)· M (y);
5) математическое ожидание отклонения случайного числа от его математического ожидания равно нулю:
M [ x – M (x)] = 0.
Мерой рассеяния отдельных результатов, полученных по формуле (1) или (4), около их среднего значения служит второй центральный момент. Общее правило образования центральных моментов записывается следующим образом:

откуда сразу видно, что первый центральный момент тождественно равен нулю:
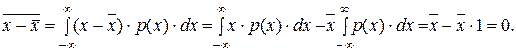
Второй центральный момент называется дисперсией и обозначается 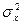 :
:
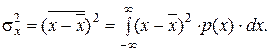
Иногда дисперсию удобнее обозначать символом D (х).
Свойства дисперсии:
1) дисперсия неслучайного числа равна нулю:
D (a) = 0;
2) постоянный множитель можно выносить за знак дисперсии, возводя его при этом в квадрат:
D (a · x) = a 2· D (x);
3) дисперсия алгебраической суммы двух случайных чисел
 ,
,
где коэффициент корреляции
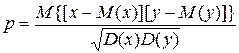 ;
;
4) дисперсия алгебраической суммы независимых случайных чисел равна арифметической сумме их дисперсий:
D (x + y – z) = D (x)+ D (y)+ D (z);
5) дисперсия случайного числа равна разности между математическим ожиданием его квадрата и квадратом математического ожидания:
D (x) = M (x 2) – M 2(x).
Чем больше дисперсия, тем значительнее рассеяние результатов, полученных по формулам (1), (4) относительно 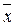 .
.
В метрологии в качестве меры рассеяния чаще используют среднее квадратическое отклонение:
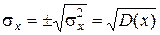 .
.
Находит применение и третий центральный момент:
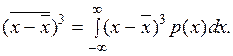
Мерой несимметричности распределения вероятности служит асимметрия:
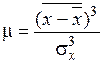 ,
,
которая может быть положительной и отрицательной. Для симметричных распределений вероятности отсчета асимметрия равна нулю
Четвертый центральный момент используется для оценки заостренности дифференциальной функции распределения вероятности. Мерой заостренности служит эксцесс:
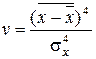 ,
,
равный трем у закона распределения вероятности отсчета, кривая плотности вероятности которого имеет колоколообразную форму. Кривые с более острой вершиной имеют больший эксцесс, с более пологой – меньший, вплоть до отрицательного.
Мерой неопределенности случайного числа является энтропия (мера хаоса):
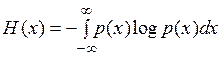 .
.
Это среднее значение логарифма плотности вероятности, взятое со знаком минус. Так как P (х)< 1, то энтропия всегда положительна. Она равна нулю у неслучайного числа и максимальна при равномерной плотности распределения вероятности.
Дифференциальная и интегральная функции (F (x i), P (x i)) распределения вероятности и все моменты обладают важным качеством: будучи характеристиками случайного числа, сами они не являются случайными.
Таблица 1
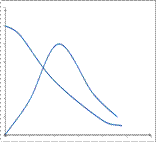
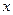 -распределение
модуля многомерного
вектора -распределение
модуля многомерного
вектора
|
|
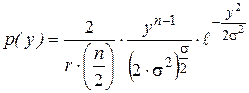
|
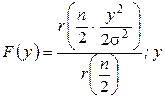 >0 >0
|
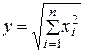
| |
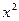 -
распределение
(Пирсона) -
распределение
(Пирсона)
| 
|
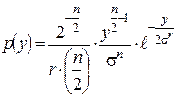
|
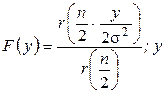 >0 >0
| При 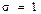
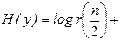
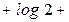
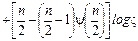 Где
Где 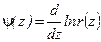 -
Пси –функция
Эйлера -
Пси –функция
Эйлера
|
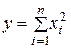
|
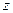 -
распределение -
распределение
| 
|

|
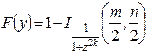
|
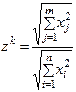
|
 Наиболее распространенной формой плотностью распределения вероятности результатов измерений во многих природных процессах является так называемое нормальное распределение (распределение Гаусса) (рис.9). Некоторые из законов распределения вероятности результатов измерений представлены в табл. 1
Наиболее распространенной формой плотностью распределения вероятности результатов измерений во многих природных процессах является так называемое нормальное распределение (распределение Гаусса) (рис.9). Некоторые из законов распределения вероятности результатов измерений представлены в табл. 1






