Любое измерение по шкале отношений предполагает сравнение неизвестного размера Q с известным [ Q ] и выражение первого через второй в кратном (дольном) отношении:
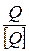 .
.
Если измерение линейного размера выполняется при помощи микроскопа, мы имеем некоторое увеличение n и измеряемая величина Q увеличивается в n раз. А когда в деле появляется тара (например, для сыпучих веществ), то масса измеряемой величины будет измерена вместе с массой тары. В первом случае мы имеем дело с мультипликативной, а во втором – с аддитивной поправками:
 ;
;  .
.
Таким образом, само сравнение, происходит под влиянием множества случайных и неслучайных аддитивных (суммарных) и мультипликативных факторов, точный учет которых невозможен, а результат совместного воздействия непредсказуем. Ограничиваясь для простоты аддитивными воздействиями, совместное влияние которых можно учесть случайным слагаемым η, получим уравнение измерений по шкале отношений:
 , (1)
, (1)
где h, X – случайные величины и, соответственно, коэффициент, учитывающий влияние факторов и некоторый отсчет по шкале (случайное число).
Эта процедура сравнения и есть измерение.
Из-за случайного характера h отсчет по шкале отношений Х получается все время разный. Это фундаментальное положение является законом природы. На основании громадного опыта практических измерений может быть сформулировано следующее утверждение, называемое основным постулатом метрологии: «Отсчет является случайным числом».
Уравнение (1) является математической моделью по шкале отношений. Отсчет в ней представлен одним числом. Отсчет может быть представлен словами, математическим символом, массивом экспериментальных данных, таблично, графически, аналитическим выражением и т. п.
После выполнения измерительной процедуры в уравнении (1) остается два неизвестных: Q и h.
Неслучайное значение аддитивной поправки ν либо должно быть известно до измерений, либо устанавливаться посредством дополнительных исследований. Слагаемое h является случайным и не может быть известным в принципе, поэтому определить значение измеряемой величины Q невозможно:
 . (2)
. (2)
Равенство (2) соблюдается точно благодаря тому, что при повторных выполнениях измерений случайное изменение второго слагаемого влечет за собой изменение первого. О таких слагаемых говорят, что они коррелированны (взаимосвязаны между собой). Разность между коррелированными значениями двух случайных величин неслучайна, но в данном случае неизвестна. Поэтому строгого решения уравнение (2) не имеет.
На практике удовлетворяются приближенным значением Q. Для этого используют результаты специального исследования, называемого метрологической аттестацией средства измерений и методики выполнения измерений, в ходе этого исследования приближенно определяется среднее значение второго слагаемого в правой части уравнения (2):
 .
.
Среднее значение не является случайным, поэтому после замены случайного второго слагаемого неслучайным значением Н получается приближенное решение, в котором результат измерения Q является случайным значением измеряемой величины:
 . (3)
. (3)
Первое слагаемое в правой части выражения (3) называется показанием: Х=Х· [ Q ]. Оно подчиняется тому же закону распределения вероятности, что и отсчет, но отличается от последнего тем, что dim X = dim Q. Два последних слагаемых в правой части (3) представляют собой суммарную поправку:
 ,
,
которая может включать и большее количество составляющих, в зависимости от числа учитываемых факторов. Поправка не является случайной, но может изменяться от измерения к измерению по определенному закону. Поэтому в каждое отдельное значение показания X i может вноситься своя поправка θ i.
Результат измерения Q подчиняется тому же закону распределения вероятности, что показания и отсчет, но смещенному по оси абсцисс на значение суммарной поправки. Отдельное его значение Q i = X i+θ i, получаемое всякий раз после выполнения измерительной процедуры, называется результатом однократного измерения.
Среднее арифметическое значение результата измерения, полученное при многократном независимом измерении одной и той же величины постоянного размера, называется результатом многократного измерения и определяется по формуле:
 ,
,
где n – число измерений.
Уравнение измерения по шкале интервалов записывается аналогично уравнению (1):
 (4)
(4)
где Δ Q – значение разности между двумя размерами физической величины. Анализ этого уравнения не отличается от анализа уравнения (1).
Математической моделью измерения по шкале порядка служит неравенство, где сравнивают Q 1 + η 1 и Q 2 + η 2, описывающее процедуру сравнения двух размеров одной и той же величины. Результатом сравнения в этом случае является не отсчет, а решение о том, какой из размеров больше, либо они одинаковы. Не исключена возможность, как правильных, так и неправильных решений. Отсюда результат сравнения двух размеров по шкале порядка является случайным, что соответствует основному постулату метрологии.
Измерения по шкале порядка широко применяются при контроле, когда Q 1 сравнивается с контрольным (пороговым) Q 2 в условиях случайных возмущений. Особое место занимает сравнение с Q 2 = 0, относящееся к теории обнаружения.






