В методике Лагранжа механическую систему рассматривают как одно целое, отдельные материальные точки системы не выделяются. Уравнения Лагранжа II рода показывают скорость изменения меры движения системы (кинетической энергии).
Сравнивая (А) и (В) можно объяснить преобразования, которые выполнялись затем над уравнением (6).
2. Количество уравнений движения системы, как видно из (В), будет столько, сколько степеней свободы имеет механическая система, и, в случае голономных реакций связи, равняется числу обобщённых координат S. Их количество не будет зависеть от количества точек «n», входящих в систему. Для уравнения Лагранжа I рода:
, где 
- множитель Лагранжа
всё наоборот - (количество уравнений зависит от количества точек «n», входящих в систему), что является одной из причин введения обобщённых координат. Из общего уравнения динамики (2) явно не видно количества уравнений движения.
3. Уравнения Лагранжа II рода исключают из уравнений реакции идеальных связей и это позволяет вторую задачу динамики разложить на два этапа:
а) вначале найти закон движения 
. Дифференцируя дважды уравнение движения мы находим ускорение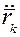 
k-той точки.
б) затем, зная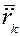 
, приложенные к системе силы 
и массу 
, можем определить реакции неизвестных связей 
из уравнения: 
4. Форма уравнений Лагранжа II рода не зависит от конкретного выбора обобщённых координат и принципиально важно:
