(общие уравнения динамики в обобщённых координатах) вар. 2.
Общее уравнение динамики в векторной форме:
(А)
даёт возможность составлять дифференциальное уравнение движения системы, при этом в него не входят реакции идеальных связей, так как перемещения на этих связях перпендикулярны направлениям векторов силы идеальных реакций связи (это следует из самого определения «идеальной связи») и по этой причине работы идеальных реакций на их перемещениях всегда равны 0: 
Где 
- векторы активных задаваемых сил и, в том числе, сил трения в связях, действующие на k-тую материальную точку системы;
- вектор силы инерции, возникающей в k-той материальной точке системы;
- элементарное перемещение радиус-вектора k-той материальной точки системы;
- вектор силы идеальной двусторонней связи;
В декартовой системе координат уравнение (А) имеет вид:
(1)
Однако, когда система материальных точек имеет несколько степеней свободы, пользоваться уравнением (1) не всегда удобно, так как вариации декартовых координат взаимосвязаны между собой. Тогда удобнее пользоваться обобщёнными координатами, которые независимы друг от друга и независимы и их вариации.
Итак, нужно общее уравнение динамики (А), записанное в векторной форме:
(А) или 
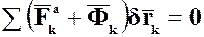(2)
записать в обобщённых координатах.
Рассматриваем движение несвободной механической системы, состоящей из n точек, на которую наложены идеальные, стационарные и удерживающие связи. Будем полагать, что система имеет S степеней свободы и в случае голономных связей число обобщенных координат равно S степеней свободы. Таким образом положение k-той точки будет определяться радиус-вектором 
, который является функцией всех обобщенных координат 
: 
(3) тогда элементарное приращение радиус-вектора k-той точки по j-той обобщенной координате равняется: 
, где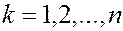 
; 
и в развёрнутом виде элементарное приращение радиус-вектора k-той точки по всем обобщенным координатам S равняется: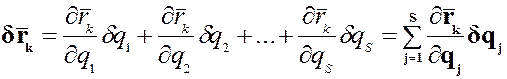 
(4)
Подставляем значение элементарного приращения радиус-вектора k-той точки 
из уравнения (4) в уравнение (2):
(5)
подставим значение силы инерции k-той точки 
, поменяем порядок суммирования и знаки в обоих частях равенства (5):
(6)
выразим скорость k-той точки через её частные производные по обобщённым координатам 
и обобщенным скоростям 
:
(7)
где
возьмём от (7) частную производную по обобщенной скорости 
:
получим 
(8)
Пояснение:
все составляющие уравнения (7) не зависят от частной производной по скорости обобщенной координаты и при дифференцировании по превращаются в 0. Остается только дифференциал 
В дальнейшем выполним следующие преобразования:
1) в первом слагаемом уравнения (6) заменим, в соответствии с (8),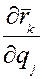 
на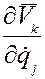 
и покажем это произведение двух дифференциалов в следующем виде:
(9)
Пояснение: Это равенство возможно, так как справедливо следующее преобразование: 
2) продифференцируем по времени равенство (8):
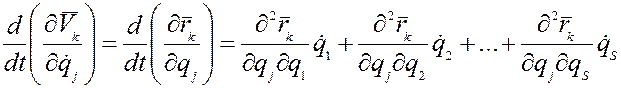(10)
Пояснение:
Покажем процесс дифференцирования в уравнении (10) на примере первого слагаемого:
и так далее,
3) найдем частную производную скорости k-той точки в равенстве (7) по обобщенной координате 
:
(11)
Правые части уравнений (10) и (11) равны. Следовательно, равны и левые части.
То есть: 
(12)
В уравнении (9) первое слагаемое правой части запишем, внеся скорость 
под знак дифференциала 
, а во втором слагаемом, воспользовавшись уравнением (12):
, заменим 
на 
.
В результате этих преобразований получим:
(13)
Заменим первое слагаемое в левой части уравнения (6) правой частью равенства (13) 
(13-2)
Знак суммирования 
введем в скобки первого и второго слагаемых равенства (13-2):
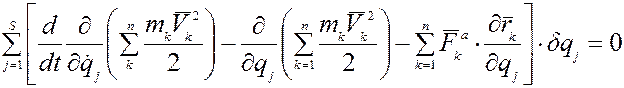(13-3)
Введем понятие обобщенной силы 
(как до этого мы ввели понятие обобщенной координаты 
).
Обобщенной силой , соответствующей обобщенной координате , называют скалярную величину, определяемую отношением элементарной работы 
действующих сил на перемещении механической системы, вызванном элементарным приращением 
обобщенной координаты , к величине этого элементарного приращения : 
.
Введем понятие элементарной работы: 
,
где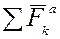 
- сумма активных задаваемых сил, действующих на k-тую точку системы,
- элементарное приращение радиус-вектора k-той точки системы,
Введем понятие кинетической энергии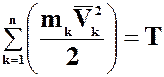 
, и заменим в уравнении (13-2) в первом и втором слагаемых дроби в круглых скобках: 
, обозначающим их значком кинетической энергии 
, а третье слагаемое заменим обозначением обобщенной силы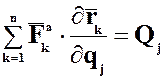 
, учитывая, что элементарная работа равна .
Тогда уравнение (13-3) примет окончательный вид:
(13-4)
Так как вариации элементарного приращения обобщенной координаты (степени свободы системы: j=1, 2, 3,… s) – произвольные независимые и не равные нулю, то уравнение (13-4) упрощается и, после сокращения 
, окончательно получим уравнение Лагранжа II рода: 
(В) (14)
где j=1, 2, 3,… s – степени свободы механической системы,
- частный дифференциал кинетической энергиисистемы по скорости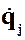 
j-тойобобщенной координаты .
- частный дифференциал кинетической энергиисистемы по j-тойобобщенной координате .
- обобщенная сила, соответствующая обобщенной координате ,
Найдём значение для консервативных систем сил (когда силы, действующие на механическую систему, имеют потенциал).
Составим сумму работ всех сил, действующих на систему, на возможных элементарных перемещениях радиус-вектора точек 
, вызванных элементарным приращением обобщенной координаты 
. Воспользуемся для этого выражением элементарной работы силы в виде скалярного произведения силы на элементарное приращение обобщенной координаты: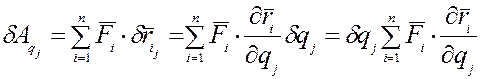 
(15)
Где элементарные приращения радиус-вектора точек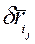 
, покажем через элементарные приращения обобщенной координаты : 
Так как обобщенной силой , соответствующей обобщённой координате , называется скалярная величина, определяемая отношением элементарной работы действующих сил, на элементарном перемещении механической системы, вызванном элементарным приращением j-той обобщенной координаты , к величине этого приращения, то формула обобщённой силы будет иметь следующий вид:
(16)
Подставив (15) в (16) получим обобщённую силу в виде суммы скалярных произведений векторов силы на частный дифференциал радиус-вектора 
i-той точки системы по j-той обобщенной координате :
(17)
Выразим это скалярное произведение через проекции векторов на декартовые оси координат:
(18)
В том случае, когда силы 
, действующие на механическую систему, имеют потенциал, тогда проекции этих сил на оси координат равны взятым с обратным знаком частным производным от потенциальной энергии системы 
по соответствующим координатам точек:
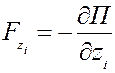(19)
Подставим это значение проекций сил в формулу (18):
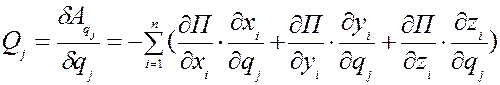(20)
Найдём частную производную от потенциальной энергии системы по обобщённой координате , рассматривая как сложную функцию обобщённых координат, определяемую зависимостями:
,
где 
Эта частная производная от потенциальной энергии определяется суммой 3n слагаемых:
(21)
Так как правые части уравнений (20) и (21) равны, то равны соответственно и левые части: 
(22)
Подставим значение обобщённой силы из уравнения (22) в уравнение Лагранжа II рода (14) и получим уравнение Лагранжа II рода для консервативных систем сил (когда силы, действующие на механическую систему, имеют потенциал).
:
(23)
ВЫВОДЫ
1. Ньютоновский метод исследования движения механической системы основан на векторной мере движения – количестве движения материальной точки: 
. Эта мера требует введения понятия силы (и меры силы - импульса силы 
)
