Особенности напряженного состояния вязкой жидкости.
Нормальные и касательные напряжения. Тензор напряжений.
Закон трения Ньютона. Законом трения Стокса.
Поперечный и продольной градиент скорости.
Динамический и кинематический коэффициент вязкости.
Скорости угловой и линейной деформации. Тензор скоростей деформаций
Давление в вязкой жидкости. «Вторая вязкость».
Уравнение Навье Стокса.
Уравнения движения идеальной жидкости рассматривались в разделе Уравнения движения[1], где они были представлены в форме Эйлера и в форме Громеки. В настоящем разделе изучается движение вязкой жидкости. Это более сложное явление. В отличие от идеальной жидкости, где поверхностными силами являются только силы нормального давления (нормальные напряжения сжатия), в вязкой жидкости эти силы получаются несколько иными, а именно: появляются касательные напряжения, приложенные к поверхностям, которые ограничивают рассматриваемый объем, нормальные напряжения зависят не только от давления, но и от сил вязкости.
Уравнения движения вязкой жидкости выводятся тем же методом, что и уравнения Эйлера, только расширяется комплект действующих сил — добавляются касательные напряжения, а нормальные напряжения вычисляются более сложно. Поэтому, прежде чем приступить к выводу, необходимо выяснить, как определяются напряжения.
В элементарном объеме, изображенном на рисунке 5, полагая, что жидкость вязкая, векторы поверхностных сил будут направлены не перпендикулярно к площадкам (например, АDЕF, ВСКL), а под косыми углами к ним. Это связано с тем, что векторы напряжений поверхностных сил имеют не только нормальные компоненты, но и касательные. Заметим также, что в теории вязкой жидкости положительными нормальными напряжениями считаются напряжения растяжения. Поэтому на схемах подобных рисунку 5, напряжения от поверхностных сил изображают векторами, направленными не внутрь рассматриваемого объема, а наружу.
Для обозначения проекций вектора напряжения поверхностной силы применяется двойная индексация. Первый индекс указывает ту площадку, на которой рассматриваются напряжения. Этому индексу дается наименование той координатной оси, которая нормальна к заданной площадке. Так, например, для площадки, параллельной координатной плоскости хоу, при обозначении любых напряжений первым индексом будет z. Второй индекс указывает ту ось, на которую проектируется вектор напряжения. Таким образом, на каждой площадке рассматриваются два касательных и одно нормальное напряжение. Касательные имеют разноименные индексы, нормальные — одноименные (см. рисунок 109).
Поскольку частицу жидкости можно представить как элементарный объем кубической формы, то вполне очевидно, что для характеристики ее напряженного состояния нужно задать следующие девять величин:
pxx τyx τzx
τxy pyy τzy
τxz τyz τzz
Если составить моменты сил, вызываемые касательными напряжениями, приложенными к граням кубика, и рассмотреть условия их равновесия относительно координатных осей [2], то нетрудно доказать, что
τxy = τyx,
τyz = τzy,
τzx = τxz,
т.е. касательные напряжения, приложенные к смежным граням и действующие в одной плоскости, численно равны. Это дает значительное упрощение, так как позволяет сократить число рассматриваемых напряжений с девяти до шести.
Для дальнейших рассуждений необходимо связать напряжения со скоростью движения жидкости.
Наиболее простую зависимость касательных напряжений от скорости дает закон жидкостного трения Ньютона
(6.1)
Здесь τ — касательное напряжение, ∂w/∂n — изменение скорости по нормали к линии тока, или поперечный градиент скорости. Коэффициент пропорциональности в этой формуле μ — называется динамическим коэффициентом вязкости, или динамической вязкостью. Он зависит от рода жидкости и характеризует вязкость. Кроме того, он зависит от температуры. Для капельных жидкостей с ростом температуры и уменьшается, следуя зависимости
(6.2)
где а и b — постоянные для данного рода жидкости коэффициенты, t — температура в градусах Цельсия, μ 0 — динамический коэффициент вязкости при t=0°. Для газов μ возрастает с увеличением температуры. Эта зависимость хорошо описывается формулой Сатерлэнда
(6.3)
в которой с — коэффициент, зависящий только от рода газа, Т — абсолютная температура в градусах Кельвина, μ 0 — коэффициент вязкости при Т=Т0. Для воздуха можно пользоваться также приближенной зависимостью
(6.4)
Наряду с динамическим коэффициентом вязкости применяется еще кинематический коэффициент вязкости
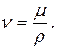(6.5)
Его размерность [ м2/сек ] не содержит динамических величин, а только кинематические, откуда он и получил свое название.
Единицы измерения для μ и ν в различных системах следующие:
| СИ | СГС | МКГС (техническая) | |
| μ | 1 
| 1 
| 1 
|
| ν | 1 
| 1 
| 1
|
В системе СГС эти единицы имеют специальные названия: 1 дин сек/см2 = 1 пуаз; 1 см2/сек = 1 стокс. Соотношение между единицами в различных системах такое:
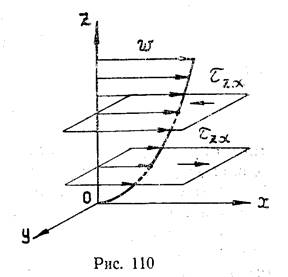
Применяя формулу Ньютона (6.1) к потоку, движущемуся параллельно плоскости хоу (см. рисунок 110), можно записать
(6.6)
Если рассмотреть два бесконечно близко расположенных слоя, которые на рисунке 110 изображены параллельными плоскостями, то можно заметить, что касательные напряжения на верхний слой со стороны нижнего действуют против движения, а на нижний со стороны верхнего — по движению. Иначе говоря, верхний слой стремится увлечь за собой нижний, а нижний слой тормозит верхний. Объем жидкости, находящийся между такими слоями, деформируется, получая деформацию сдвига (см. рисунок 111). Согласно формуле (1.5)[3] скорость угловой деформации определится как
что при 
= 0 (так как wz=0) даст
Тогда
(6.7)
Таким образом, между касательным напряжением и скоростью угловой деформации существует линейная зависимость с коэффициентом пропорциональности 2μ.
В более общем виде связь между напряжениями и скоростями деформации жидкости устанавливается законом трения Стокса. Этот закон имеет формальную аналогию с законом Гука для твердого тела, применяемом в теории упругости или в сопротивлении материалов. По закону Гука напряжения, возникающие в твердом теле, пропорциональны деформациям: нормальные напряжения пропорциональны линейным относительным деформациям, а касательные — угловым. Согласно закону Стокса напряжения пропорциональны не деформациям, а скоростям деформации: нормальные — скорости линейной деформации, а касательные — скорости угловой деформации. Коэффициент пропорциональности, как это следует из рассмотренного выше частного примера, равен 2μ [4].
Обращаясь к теореме Коши-Гельмгольца (1.7)[5] видим, что при движении жидкого объема в общем случае имеют место следующие скорости деформации:
скорости линейной деформации 
скорости угловой деформации 
Тогда, принимая во внимание формулы (1.5), можно записать касательные напряжения в таком виде:
(6.8)
а нормальные напряжения, возникающие только от действия сил вязкости, представить так:
(6.9)
Нужно обратить внимание, что полные величины нормальных напряжений рхх, руу, рzz отличаются от записанных формулой (6.9) на величину давления в газе р0, которое определяется молекулярно-кинетическими процессами. (Давление в газе или жидкости существует и тогда, когда влияние вязкости отсутствует, например, в идеальной жидкости или в неподвижной реальной жидкости). Таким образом,
(6.10)
Знак минус перед величиной р0 связан с тем, что давление создает напряжения сжатия, в то время как положительными считаются нормальные напряжения растяжения.
Вычитая из утроенной величины рxх сумму напряжений, можно записать
откуда
(6.11)
Теперь следует ввести понятие о том, что такое давление в вязкой жидкости.
Если за величину давления принять нормальные напряжения рхх, рyy, рzz, то возникает неудобство, так как в одной и той же точке эти напряжения различны по величине. В этом случае пришлось бы в каждом направлении рассматривать свою величину давления. Для того чтобы понятия давления в вязкой жидкости и в идеальной жидкости сохранялись идентичными, надо отыскать такую комбинацию, составленную из трех напряжений рхх, рyy и рzz, которая не зависела бы от ориентации системы координат, иначе говоря, которая не зависела бы от ориентации площадки, проведенной внутри жидкости для подсчета действующих на нее сил давления. Таким свойством обладает средняя арифметическая величина
р = – (рхх + рyy + рzz)/ 3. (6.12)
Она и принимается в качестве давления в вязкой жидкости.
Пользуясь таким представлением о давлении, можно записать выражение (6.11) для рхх и аналогичные ему для рyy и рzz в следующем виде:
(6.13)
В случае несжимаемой жидкости, согласно уравнению неразрывности divw=0, тогда последние слагаемые в правой части обращаются в нуль и уравнения (6.13) упрощаются. Сопоставляя их с формулами (6.10), нетрудно заметить, что в этом случае р=р0.
Попутно заметим, что «давление движущейся жидкости имеет свойства гидростатического, если не учитывать сил вязкости. Действительно, для невязкой жидкости силы, являющиеся причиной движения, не отличаются от сил, действующих в покоящейся жидкости (массовые силы, силы инерции). Поэтому доказательство того, что давление образует скалярное поле (см. Гидростатику), полностью распространяется и на движущуюся невязкую жидкость ».
& (Смыслов) с.83 … 84
Для вывода уравнений движения вязкой жидкости рассмотрим элементарный объем АВСDЕFLК (см. рисунок 112), движущийся под действием сил: поверхностных нормальных 
, поверхностных касательных 
и массовых 
. Равнодействующая этих сил, в соответствии со вторым законом Ньютона, должна равняться массе жидкого объема, умноженной на ускорение. Запишем это уравнение сначала в проекциях на ось x, подсчитав предварительно проекции действующих сил
Получим
здесь 
— масса, а 
— проекция ускорения на ось х. После подстановки сюда вычисленных значений проекций сил, приведения подобных и сокращения на 
, это уравнение приобретает вид:
(6.14)
Подставим теперь вместо напряжений их выражения через скорости деформаций, пользуясь формулами (6.13) и (6.8) и считая μ=соnst. Тогда
и уравнение (6.14) после небольших преобразований принимает такой вид:
Применяя здесь операторы Δ и div
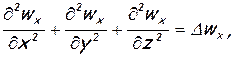
запишем
Поделив обе части равенства на ρ и приняв во внимание, что 
, представим уравнение движения в проекциях на ось х и аналогичные ему в проекциях на оси у и z в окончательном виде
(6.15)
Они называются уравнениями Навье-Стокса [6].
В заключение нужно отметить, что существует кроме зависимости (6.12) еще одна, которая может представлять давление в вязкой жидкости, а именно
р = – (рхх + рyy + рzz)/3 – μ' divw. (6.16)
Эта величина также не зависит от ориентации площадки, на которую рассматривается действие сил давления. Коэффициент μ' называется второй вязкостью.
На формальную возможность такого представления давления указывали еще Стокс и Кирхгоф, однако физическое истолкование явление второй вязкости получило в 1937 году в работах Л.И.Мандельштама и М.А.Леонтовича. Вторая вязкость связана с явлениями неравновесности и проявляется в быстропротекающих процессах. Если в движущемся газе происходит очень быстрое изменение плотности, то наблюдается некоторое отставание в изменении других величин. Восстановление равновесия протекает с диссипацией энергии, т.е. с необратимым преобразованием части энергии в тепло. Таким образом, этот эффект аналогичен вязкости.
Если провести вывод уравнений Навье–Стокса, воспользовавшись формулой (6.16) вместо (6.12), то они принимают такой вид:
(6.17)
Нужно заметить, что в несжимаемой жидкости вторая вязкость не проявляется (div w=0), а в газах при сравнительно медленных процессах последний член в формуле (6.16) мал, поэтому в обычных случаях давление в вязкой жидкости определяют по формуле (6.12), а уравнения Навье - Стокса берут в форме (6.15).
«Дифференциальные уравнения газовой динамики, записанные в координатной форме, сложны, их вывод требует большого времени и большого количества бумаги. Значительно удобнее при их получении использовать векторную алгебру и самые начала тензорного анализа: тензорные обозначения и простейшие тензорные преобразования».
& (Ден) с.13
