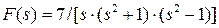Всякая несократимая дробь 
, где коэффициенты 
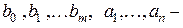некоторые действительные числа (коэффициент при старшем члене знаменателя мы делаем равным 1, деля на него числитель и знаменатель) может быть единственным образом преобразована в сумму элементарных дробей вида 
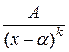или 
, если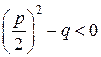 
.
При этом возможны четыре случая (см. [4 ] cтр.130).
а). Знаменатель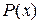 
такой, что уравнение 
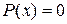имеет только действительные однократные корни 
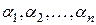. Разложение ведется по формуле: 
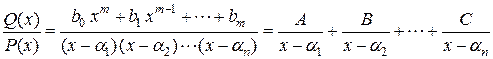, где коэффициенты 
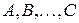определяются формулами:
, 
, …, 
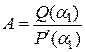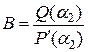(в знаменателях – значения производной 
при 
)
Пример: 
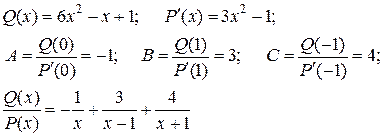
Другой способ определения 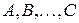- метод неопределенных коэффициентов (применяется во всех четырех случаях)
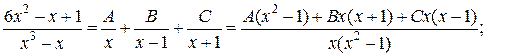
Приравнивая коэффициенты при одинаковых степенях 
числителей в левой и правой частях равенства, получаем систему уравнений:
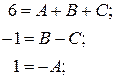
Решая ее, находим для 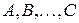те же значения, что и выше.
б). Корни знаменателя действительные, но среди них есть кратные.
Разложение ведется по формуле 
Пример: 
Коэффициенты 
находятся методом неопределенных коэффициентов.
в). Среди корней знаменателя есть комплексные, однократные.
Разложение ведется по формуле 
Пример: 
Коэффициенты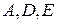 
находятся методом неопределенных коэффициентов.
г). Среди корней знаменателя есть комплексные, кратные.
Разложение ведется по формуле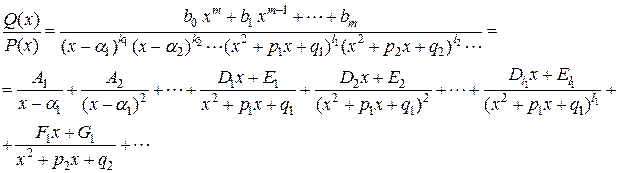 
Пример: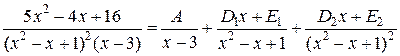 
Коэффициенты 
находятся методом неопределенных коэффициентов.
3. Задание. Вычислить обратное преобразование Лапласа функции
