Косвенными называются измерения, при которых измеряемая величина у определяется как функция нескольких величин х1, х2, … хn:
y = f(х1, х2, … хn). (16)
При этом предполагается, что все аргументы независимы и измерены независимыми способами.
Наиболее вероятное значение косвенно измеряемой величины, <y>
<y> = f(<х1>, <х2>, … <хn>). (17)
Погрешность косвенного измерения определяют погрешности прямых измерений аргументов
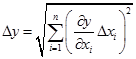, (18)
где Dxi – полные погрешности величин xi, 
– частные производные функции (16) по аргументам xi, взятые в предположении, что остальные аргументы постоянны. Если доверительная вероятность результатов измерений xi равна р, то такой она будет и для Dу.
Относительная погрешность косвенных измерений величины у:
. (19)
Если функция содержит аргументы в виде сомножителей, то проще сначала вычислить относительную погрешность. Зная eу находят абсолютную погрешность
Dy = eу <y>, (20)
где Dу – абсолютная погрешность косвенно измеряемой величины у.
Планирование эксперимента
До начала измерений необходимо оценить максимальную точность определения искомой величины по значениям приборной погрешности (Dхпр) и погрешности округления (Dхокр). Это достигается одним контрольным измерением и оценкой приборных погрешностей округления. Случайные погрешности увеличивают полную погрешность, но они могут быть уменьшены путём увеличения числа наблюдений (практически достаточно равенства Dхсл = Dхпр).
Пример. Необходимо определить объём цилиндра
, (21)
где d – диаметр цилиндра, h – его высота. Относительная погрешность определения объёма не должна превышать 1%.
Проводим контрольное измерение: d = 6,40 мм, h = 20,8 мм. Высота h измерена штангенциркулем, диаметр d – микрометром. Объём цилиндра
. (22)
В формулу определения объёма цилиндра все аргументы входят сомножителями. Поэтому расчёт относительной погрешности значительно проще, чем абсолютной. В соответствии с (19)
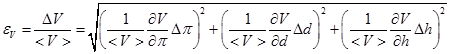. (23)
Константа p не считается постоянной, так как для расчётов используется её приближённое значение. Следовательно, при округлении допускается погрешность.
Найдём слагаемые выражения (23):
; 
; 
.
Следовательно,
. (24)
Для оценки минимальной погрешности выражение (24) примет вид
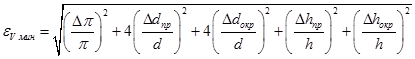. (25)
Найдём приборные ошибки и ошибки округления для используемых штангенциркуля (с = 0,1) и микрометра (с = 0,01) из таблицы (3) и формул (4) и (5):
, 
, (26)
, 
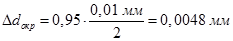. (27)
Пусть p =3,14. Тогда
Dpокр = 0,005. (28)
Подставив значения найденных величин в (25), получим
. (29)
Для оценки случайной погрешности производим 10 наблюдений d и h (см. таблицу 3).
Таблица 3. Результаты измерений для оценки случайной погрешности
| №№ п/п | d, мм | Dd, мм | h, мм | Dh, мм |
| 6,40 | -0,023 | 20,8 | 0,12 | |
| 6,42 | -0,003 | 20,4 | -0,28 | |
| 6,41 | -0,013 | 20,7 | 0,02 | |
| 6,43 | 0,007 | 20,9 | 0,22 | |
| 6,44 | 0,017 | 20,5 | -0,18 | |
| 6,42 | -0,003 | 20,8 | 0,12 | |
| 6,44 | 0,017 | 20,5 | -0,18 | |
| 6,43 | 0,007 | 20,8 | 0,12 | |
| 6,41 | -0,013 | 20,9 | 0,22 | |
| 6,43 | 0,007 | 20,5 | -0,18 | |
| Среднее | 6,42 3 | 20,6 8 |
<V> = 669,4 мм3. (30)
Случайные погрешности прямых измерений
. (31)
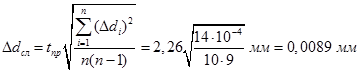. (32)
Относительная случайная погрешность косвенных измерений
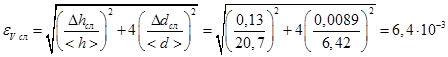, (33)
то есть
eсл = 0,64%. (34)
Полная относительная погрешность определения объёма цилиндра
. (35)
Абсолютная погрешность определения объёма
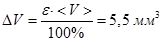. (36)
Измерение высоты цилиндра штангенциркулем, диаметра – микрометром и десять наблюдений обеспечили требуемую в задаче точность определения объёма.
Результат измерения запишем следующим образом:
V = (670 ± 6) мм3, e = 0,8% при р = 0,95. (37)
4. Измерение объёмов тел правильной формы
Для измерения линейных размеров часто используют штангенциркули и микрометры. Точность полученных результатов во многом зависит от правильной методики измерения и умения правильно пользоваться прибором. Так, для учёта не вполне правильной формы тела повторные измерения одной и той же величины необходимо производить в разных местах тела, рукоятку микрометра вращать только за головку, чтобы обеспечить небольшое и одинаковое давление на измеряемый объект.
Задание 1. Определение объёма шара
Объём шара
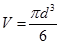, (38)
где d – диаметр шара. Погрешность определения объёма не должна превышать 2%.
1. С помощью микрометра проводят контрольные измерения диаметра шара d.
2. Оценивают минимальную погрешность в определении объёма шара.
3. Проводят ряд повторных измерений. Находят <d> и Ddсл.
4. По (38) определяют объём шара.
5. Оценивают погрешность измерений.
Задание 2. Определение объёма параллелепипеда
Объём параллелепипеда
V = a×b×h, (39)
где a – длина параллелепипеда, b – его ширина, h – высота.
Погрешность определения объёма не должна превышать 6%.
1. С помощью штангенциркуля проводят контрольное измерение величин a, b, h.
2. Оценивают минимальную погрешность в определении объёма
. (40)
3. Проводят ряд повторных наблюдений a, b, h, находят их средние значения и случайные погрешности.
4. По (39) определяют объём параллелепипеда.
5. Оценивают погрешность измерения.
Контрольные вопросы
1. Какие ошибки возможны при прямых измерениях?
2. От каких величин зависит стандартное отклонение?
3. Что такое доверительный интервал, доверительная вероятность?
4. Как устроен нониус?
5. Каков принцип работы микрометра?
6. Какие погрешности необходимо учитывать при косвенных измерениях? Каким образом?
7. Каковы правила округления конечного результата прямых и косвенных измерений?
