В большинстве при повторении одного и того же измерения в одинаковых условиях результаты отличаются друг от друга. Среднее арифметическое значение измеряемой величины
 , (7)
, (7)
Где < x > – наиболее вероятное значение измеряемой величины при большом числе измерений xi. Случайные отклонения i -го измерения от среднего значения
Dxi = xi - <x>. (8)
Эти отклонения могут быть разными как по величине, так и по знаку, но при большом числе измерений подчиняются статистическим закономерностям. Закономерности распределения (разброс значений Dxi) характеризует дисперсия s2:
 . (9)
. (9)
Квадратный корень из дисперсии называется стандартным отклонением s случайной величины от истинного значения
 . (10)
. (10)
 Функция распределения f(x) для случайных отклонений, как следует из теории вероятностей, имеет вид
Функция распределения f(x) для случайных отклонений, как следует из теории вероятностей, имеет вид
 . (11)
. (11)
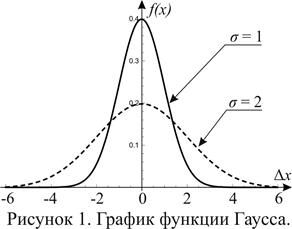
Её вид в зависимости от стандартного отклонения показан на рисунке 1. Распределение вида (11) называется нормальным или распределением Гаусса.
Как показывают расчёты, для распределения Гаусса в интервал [ <x> - s; <x> + s ] в среднем из 100 измерений попадает 68. Другими словами, вероятность попадания отдельного измерения в этот интервал равна 68%. В интервал [ <x> - 2s; <x> + 2s ] – вероятность попадания 95%, а в интервал [ <x> - 3s; <x> + 3s ] – 99,7%. Эта вероятность р называется доверительной вероятностью или надёжностью.
Если для величины х проведено n серий измерений, то средние значения каждой серии будут различны. В теории вероятностей доказывается, что стандартное отклонение для средних значений s равно
 . (12)
. (12)
Оценка стандартного отклонения по формуле (12) справедлива только для большого числа измерений. В учебных лабораториях, как правило, число измерений ограничено n = 1 ¸ 10. Для увеличения надёжности пользуются коэффициентами Стьюдента tnp (см. таблицу 2). При этом случайная погрешность прямых измерений Dхсл
 . (13)
. (13)
Таблица 2. Коэффициенты Стьюдента
| p n | 0,50 | 0,90 | 0,95 | 0,99 |
| 0,82 | 2,92 | 4,30 | 9,92 | |
| 0,77 | 2,35 | 3,18 | 5,94 | |
| 0,74 | 2,13 | 2,78 | 4,60 | |
| 0,73 | 2,02 | 2,57 | 4,60 | |
| 0,72 | 1,94 | 2,45 | 3,71 | |
| 0,71 | 1,89 | 2,36 | 3,60 | |
| 0,71 | 1,86 | 2,31 | 3,36 | |
| 0,70 | 1,83 | 2,26 | 3,25 | |
| 0,69 | 1,76 | 2,14 | 2,98 | |
| ¥ | 0,68 | 1,65 | 1,98 | 2,59 |






