Основные правила дифференцирования:
1. Производная постоянной равна нулю, т.е. 
.
2. Производная аргумента равна единице, т.е. 
.
3. Производная алгебраической суммы конечного числа дифференцируемых функций равна алгебраической сумме производных этих функций, т.е. 
.
4. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, т.е. 
.
Следствие 1. Постоянный множитель можно выносить за знак производной: 
.
Следствие 2. Производная произведения нескольких дифференцируемых функций равна сумме произведений производной каждого из сомножителей на все остальные, например: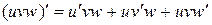 
.
5. Производная частного двух дифференцируемых функций может быть найдена по формуле 
(при условии, что 
).
6. Производная сложной функции. Пусть задана сложная функция 
.
Теорема. Если 
и 
- дифференцируемые функции от своих аргументов, то производная сложной функции существует и равна производной данной функции по промежуточному аргументу и умноженной на производную промежуточного аргумента по независимой переменной 
, т.е. 
.
Производные основных элементарных функций (таблица производных):
1. Производная логарифмической функции.
А) 
и 
, где 
- некоторая функция зависящая от .
Б) 
и 
.
2. Производная показательной функции.
А) 
и 
.
Б) 
и 
.
3. Производная степенной функции.
и 
.
4. Производная степенно-показательной функции.
.
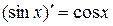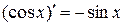5. Производная тригонометрических функций.
и 
;
и 
;
и 
;
и 
.
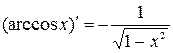7. Производная обратных тригонометрических функций.
и 
;
и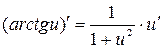 
;
и 
;
и 
.
Пример. Найти производные следующих функций:
А)  ;
| Б)  ;
|
В)  ;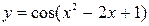
| Г)  .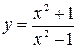
|
