Производные и дифференциалы.
Понятие производной. Уравнение касательной и нормали к плоской кривой. Непрерывность дифференцируемой функции.
Пусть на некотором промежутке 
определена функция 
. Возьмем любую точку 
. Зададим аргументу 
произвольное приращение 
такое, что точка 
также будет принадлежать . Функция получит приращение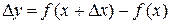 
.
Производной функции в точке называется предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (при условии, что этот предел существует), т.е. 
.
Если для некоторого значения 
выполняется условие 
или , т.е. пределы равны бесконечности, то говорят, что в точке функция имеет бесконечную производную.
Если функция имеет конечную производную в каждой точке 
, то производную 
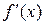можно рассматривать как функцию , также определенную на . Нахождение производной функции называется дифференцированием функции. Если функция в точке имеет конечную производную, то функция называется дифференцируемой в этой точке. Функция, дифференцируемая во всех точках промежутка , называется дифференцируемой на этом промежутке.
Задача о касательной. Пусть на плоскости 
дана непрерывная функция и необходимо найти уравнение касательной к этой кривой в точке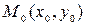 
.
Уравнение прямой по точке 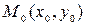, принадлежащей этой прямой, и угловому коэффициенту имеет вид: 
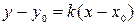, где 
, (
- угол наклона прямой).
Из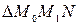 
(рис. 1) найдем тангенс угла наклона секущей 
: 
.
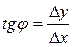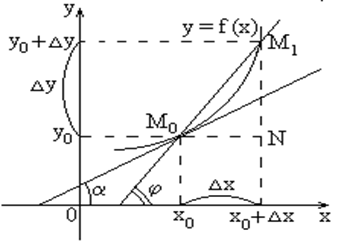
Рис. 1.
Если точку 
приближать к точке 
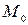, то угол 
будет стремиться к углу , т.е. при 
. Следовательно, 
.
Из задачи о касательной следует геометрический смысл производной: производная 
есть угловой коэффициент (тангенс угла наклона) касательной, проведенной к кривой в точке , т.е. 
. Следовательно, уравнение касательной к кривой в точке примет вид 
.
Нормалью к кривой в данной точке называется прямая, проходящая через данную точку, перпендикулярная к касательной в этой точке. Уравнение нормали к кривой в точке 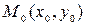имеет вид: 
.
Пример. Найти производную функции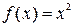 
.
Решение: Придавая аргументу приращение 
, найдем соответствующее приращение функции:
.
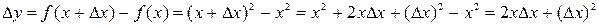Составим отношение: 
. Найдем предел этого отношения при : 
.
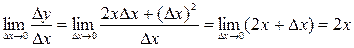Механический смысл производной. Производная пути по времени 
есть скорость точки 
в момент 
, т.е. 
.
Функция называется дифференцируемой в точке , если ее приращение 
в этой точке можно представить в виде 
, где 
– некоторое число, не зависящее от , а 
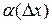– функция аргумента , являющаяся бесконечно малой при , т.е. 
.
Выясним теперь связь между дифференцируемостью в точке и существованием производной в той же точке.
Теорема. Для того чтобы функция 
была дифференцируемой в данной точке , необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Пример. Доказать, что функция 
недифференцируема в точке 
.
Решение: Производная функции (если она существует) равна 
.
При производная не существует, так как отношение 
т.е. не имеет предела при (ни конечного, ни бесконечного). Геометрически, это означает отсутствие касательной к кривой в точке .
Теорема. Если функция дифференцируема в точке , то она в этой точке непрерывна.
Обратная теорема неверна, если функция непрерывна в данной точке, то она не обязательно дифференцируема в этой точке. Так, функция непрерывна в точке 
, ибо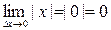 
но, как было доказано ранее недифференцируема в этой точке.
Таким образом, непрерывность функции – необходимое, но не достаточное условие ее дифференцируемости.
Замечание: Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором промежутке , то функция называется гладкой на этом промежутке. Если же производная функция допускает конечное число точек разрыва, то такая функция на данном промежутке называется кусочно гладкой.
Теорема Ролля. Пусть функция удовлетворяет следующим условиям: 1. непрерывна на отрезке 
; 2. дифференцируема на интервале 
; 3. на концах отрезка принимает равные значения, т.е. 
. Тогда внутри отрезка существует по крайней мере одна точка 
, в которой производная функции равна нулю: 
.
Геометрический смысл теоремы Ролля. При выполнении условий теоремы внутри отрезка найдется точка , в которой касательная, проведенная к графику функции , параллельна оси 
(рис. 2). Таких точек на интервале может быть и несколько, но теорема утверждает существование по крайней мере одной такой точки.
Замечание. Пусть 
. Тогда 
и 
– нули функции , и между ними найдется такая точка , что . Таким образом, из теоремы Ролля следует, что между нулями дифференцируемой функции находится хотя бы один нуль производной (рис. 3).
Рис. 2.
| 
Рис. 3.
|
Теорема Ролля является частным случаем теоремы Лагранжа.
Теорема Лагранжа. Пусть функция удовлетворяет следующим условиям: 1. непрерывна на отрезке ; 2. дифференцируема на интервале . Тогда внутри отрезка существует по крайней мере одна точка , в которой выполняется равенство: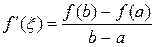 
.
Это означает, что если на некотором промежутке выполняются условия теоремы, то отношение приращения функции к приращению аргумента на этом отрезке равно значению производной в некоторой промежуточной точке.
Геометрический смысл теоремы Лагранжа заключается в том, что при выполнении условий теоремы внутри отрезка найдется точка , в которой касательная, проведенная к графику функции , параллельна хорде 
(рис. 4). Таких точек может быть и несколько, но одна существует точно.
Рис. 4.
Следствие. При выполнении условий теоремы Лагранжа 
. Эту формулу называют формулой конечных приращений.
Производная функции может быть найдена по схеме:
1) Дадим аргументу приращение 
и найдем наращение значений функции 
.
2) Находим приращение функции 
.
3) Составляем отношение 
.
4) Находим предел этого отношения при , т.е. 
(если этот предел существует).
